题目内容
11. 如图,AC=BD,AC⊥BC于C,BD⊥AD于D,AC与BD交于点E.有下列结论:①△ABC≌△BAD;②△ADE≌△BCE;③点E在线段AB的垂直平分线上.以上结论正确的有( )
如图,AC=BD,AC⊥BC于C,BD⊥AD于D,AC与BD交于点E.有下列结论:①△ABC≌△BAD;②△ADE≌△BCE;③点E在线段AB的垂直平分线上.以上结论正确的有( )| A. | ① | B. | ② | C. | ①和② | D. | ①和②和③ |
分析 依据HL可证明△ABC≌△BAD,然后依据全等三角形的性质可证明AD=BC,然后再依据AAS证明△ADE≌△BCE,然后全等三角形的性质可得到BE=AE,最后依据线段垂直平分线的性质定理的逆定理可对③作出判断.
解答 解:∵AC⊥BC于C,BD⊥AD于D,
∴∠D=∠C=90°.
在Rt△ABC和Rt△ADE中$\left\{\begin{array}{l}{AC=BD}\\{AB=AB}\end{array}\right.$,
∴Rt△ABC≌Rt△ADE.
故①正确.
∵Rt△ABC≌Rt△ADE,
∴AD=CB.
在△ADE和△BCE中$\left\{\begin{array}{l}{∠D=∠C}\\{∠DEA=∠CEB}\\{AD=BC}\end{array}\right.$,
∴△ADE≌△BCE.
故②正确.
∵△ADE≌△BCE,
∴AE=BE.
∴点E在AB的垂直平分线上.
故③正确.
故选:D.
点评 本题主要考查的是全等三角形的性质和判定、线段垂直平分线的性质定理的逆定理,熟练掌握相关知识是解题的关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
1.下面图形中不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
2.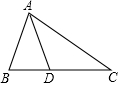 已知:如图,在△ABC中,AD是它的角平分线,AB=6cm,AC=8cm,则 S△ABD:S△ACD=( )
已知:如图,在△ABC中,AD是它的角平分线,AB=6cm,AC=8cm,则 S△ABD:S△ACD=( )
 已知:如图,在△ABC中,AD是它的角平分线,AB=6cm,AC=8cm,则 S△ABD:S△ACD=( )
已知:如图,在△ABC中,AD是它的角平分线,AB=6cm,AC=8cm,则 S△ABD:S△ACD=( )| A. | 4:3 | B. | 3:4 | C. | 16:9 | D. | 9:16 |
16. 如图,在△ABC中,D是BC边上一点,且AB=AD=DC,∠C=35°,则∠BAD为( )
如图,在△ABC中,D是BC边上一点,且AB=AD=DC,∠C=35°,则∠BAD为( )
 如图,在△ABC中,D是BC边上一点,且AB=AD=DC,∠C=35°,则∠BAD为( )
如图,在△ABC中,D是BC边上一点,且AB=AD=DC,∠C=35°,则∠BAD为( )| A. | 25° | B. | 35° | C. | 40° | D. | 50° |
 如图,已知∠AOB,求作射线OC,使OC平分∠AOB.作射线OC;在OA和OB上分别截取OD,OE,使OD=OE;分别以点D,E为圆心,以大于$\frac{1}{2}$DE长为半径,在∠AOB内作弧,两弧交于点C.
如图,已知∠AOB,求作射线OC,使OC平分∠AOB.作射线OC;在OA和OB上分别截取OD,OE,使OD=OE;分别以点D,E为圆心,以大于$\frac{1}{2}$DE长为半径,在∠AOB内作弧,两弧交于点C.