题目内容
3. 如图,已知∠AOB,求作射线OC,使OC平分∠AOB.作射线OC;在OA和OB上分别截取OD,OE,使OD=OE;分别以点D,E为圆心,以大于$\frac{1}{2}$DE长为半径,在∠AOB内作弧,两弧交于点C.
如图,已知∠AOB,求作射线OC,使OC平分∠AOB.作射线OC;在OA和OB上分别截取OD,OE,使OD=OE;分别以点D,E为圆心,以大于$\frac{1}{2}$DE长为半径,在∠AOB内作弧,两弧交于点C.上述做法合理的顺序是②③①.(写序号)
这样做出的射线OC就是∠AOB的角平分线,其依据是三边分别相等的两个三角形全等,全等三角形的对应角相等,角平分线定义.
分析 先根据角平分线的作法进行判断,再根据图形进行说理,运用全等三角形的判定与性质进行证明,进而得出结论.
解答 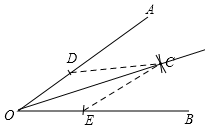 解:已知∠AOB,求作射线OC,使OC平分∠AOB.
解:已知∠AOB,求作射线OC,使OC平分∠AOB.
步骤为:
第一步:在OA和OB上分别截取OD,OE,使OD=OE;
第二步:分别以D,E为圆心,大于$\frac{1}{2}$DE的长为半径作弧,在∠AOB内,两弧交于C;
第三步:作射线OC.
故作法合理的顺序为②③①.
如图所示,连接CD,CE,
由题可得,OD=OE,CD=CE,
在△OCD和△OCE中,
$\left\{\begin{array}{l}{OD=OE}\\{CD=CE}\\{OC=OC}\end{array}\right.$,
∴△OCD≌△OCE(SSS),
∴∠COD=∠COE(全等三角形的对应角相等),
∴OC是∠AOB的平分线(角平分线定义).
故答案为:②③①,三边分别相等的两个三角形全等,全等三角形的对应角相等,.
点评 本题主要考查了角平分线的作法,正确把握角平分线的作法以及运用全等三角形的判定与性质是解题关键.

练习册系列答案
相关题目
13.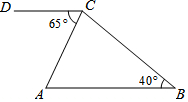 如图,△ABC中,∠B=40°,过点C作CD∥AB,∠ACD=65°,则∠ACB的度数为( )
如图,△ABC中,∠B=40°,过点C作CD∥AB,∠ACD=65°,则∠ACB的度数为( )
 如图,△ABC中,∠B=40°,过点C作CD∥AB,∠ACD=65°,则∠ACB的度数为( )
如图,△ABC中,∠B=40°,过点C作CD∥AB,∠ACD=65°,则∠ACB的度数为( )| A. | 105° | B. | 95° | C. | 85° | D. | 75° |
11. 如图,AC=BD,AC⊥BC于C,BD⊥AD于D,AC与BD交于点E.有下列结论:①△ABC≌△BAD;②△ADE≌△BCE;③点E在线段AB的垂直平分线上.以上结论正确的有( )
如图,AC=BD,AC⊥BC于C,BD⊥AD于D,AC与BD交于点E.有下列结论:①△ABC≌△BAD;②△ADE≌△BCE;③点E在线段AB的垂直平分线上.以上结论正确的有( )
 如图,AC=BD,AC⊥BC于C,BD⊥AD于D,AC与BD交于点E.有下列结论:①△ABC≌△BAD;②△ADE≌△BCE;③点E在线段AB的垂直平分线上.以上结论正确的有( )
如图,AC=BD,AC⊥BC于C,BD⊥AD于D,AC与BD交于点E.有下列结论:①△ABC≌△BAD;②△ADE≌△BCE;③点E在线段AB的垂直平分线上.以上结论正确的有( )| A. | ① | B. | ② | C. | ①和② | D. | ①和②和③ |
15.一元二次方程x(x-2)=x-2的根是( )
| A. | 0 | B. | 1 | C. | 1,2 | D. | 0,2 |
13.下列命题中,错误的是( )
| A. | 矩形的两条对角线互相平分 | |
| B. | 平行四边形的两条对角线相等 | |
| C. | 菱形的两条对角线互相垂直 | |
| D. | 等腰三角形底边上的中点到两腰的距离相等 |
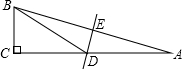 如图,在Rt△ABC中,∠ACB=90°,∠A=15°,AB的垂直平分线与AC交于点D,与AB交于点E,连结BD.若AD=10cm,则BC的长为5cm.
如图,在Rt△ABC中,∠ACB=90°,∠A=15°,AB的垂直平分线与AC交于点D,与AB交于点E,连结BD.若AD=10cm,则BC的长为5cm.