题目内容
17.已知一个二次函数y=ax2(a≠0)的图象经过(-2,6),则下列点中不在该函数的图象上的是( )| A. | (2,6) | B. | (1,1.5) | C. | (-1,1.5) | D. | (2,8) |
分析 先利用待定系数法求二次函数的解析式,再依次将各选项的点代入解析式即可作出判断.
解答 解:把(-2,6)代入y=ax2(a≠0)中得:4a=6,
a=$\frac{3}{2}$,
∴这个二次函数的解析式为:y=$\frac{3}{2}{x}^{2}$,
A、当x=2时,y=$\frac{3}{2}$×22=6,所以点(2,6)在该函数的图象上;
B、当x=1时,y=$\frac{3}{2}$×12=1.5,所以点(1,1.5)在该函数的图象上;
C、当x=-1时,y=$\frac{3}{2}$×(-1)2=1.5,所以点(-1,1.5)在该函数的图象上;
D、当x=2时,y=$\frac{3}{2}$×22=6,所以点(2,8)不在该函数的图象上;
故选D.
点评 本题考查了利用待定系数求简单的二次函数的解析式,以及判断点是否在函数图象上的方法,即代入解析式判断是否满足函数解析式.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
7. 已知实数a、b在数轴上对应的点如图所示,则下列式子正确的是( )
已知实数a、b在数轴上对应的点如图所示,则下列式子正确的是( )
 已知实数a、b在数轴上对应的点如图所示,则下列式子正确的是( )
已知实数a、b在数轴上对应的点如图所示,则下列式子正确的是( )| A. | a-b>0 | B. | a+b<0 | C. | |a|<|b| | D. | a•b>0 |
2.不等式3(x-2)≤x+4的非负整数解有( )个.
| A. | 4 | B. | 6 | C. | 5 | D. | 无数 |
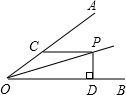 如图,∠AOP=∠OPC=15°,PC∥DO,PD⊥OB,若OC=8,则PD等于4.
如图,∠AOP=∠OPC=15°,PC∥DO,PD⊥OB,若OC=8,则PD等于4. 如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上一个动点,若PA=8,则PQ的最小值为8.
如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上一个动点,若PA=8,则PQ的最小值为8.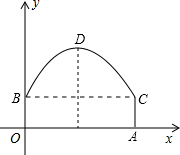 如图,隧道的截面由抛物线和长方形构成,长方形的长OA为12m,宽OB为4m,建立直角坐标系,抛物线可用y=-$\frac{1}{6}$x2+bx+c表示.
如图,隧道的截面由抛物线和长方形构成,长方形的长OA为12m,宽OB为4m,建立直角坐标系,抛物线可用y=-$\frac{1}{6}$x2+bx+c表示.