题目内容
8.已知M=$\frac{2ab}{{a}^{2}-{b}^{2}}$,N=($\frac{{a}^{2}-{b}^{2}}{{a}^{2}+{b}^{2}}$)-1,当a:b=3:2时,求M+N的值.分析 根据负指数幂的运算先化简N,根据a:b=3:2得2a=3b,代入求得M+N的值.
解答 解:∵N=($\frac{{a}^{2}-{b}^{2}}{{a}^{2}+{b}^{2}}$)-1,
∴N=$\frac{{a}^{2}+{b}^{2}}{{a}^{2}-{b}^{2}}$,
∵a:b=3:2,
∴2a=3b,
∴a=$\frac{3}{2}$b,
∴M+N=$\frac{2ab}{{a}^{2}-{b}^{2}}$+$\frac{{a}^{2}+{b}^{2}}{{a}^{2}-{b}^{2}}$,
=$\frac{(a+b)^{2}}{(a+b)(a-b)}$
=$\frac{a+b}{a-b}$
=$\frac{\frac{3}{2}b+b}{\frac{3}{2}b-b}$
=$\frac{\frac{5}{2}b}{\frac{1}{2}b}$
=5.
点评 本题考查了分式的化简求值,掌握因式分解和分式的约分是解题的关键.

练习册系列答案
相关题目
20.能把一个三角形分成两个直角三角形的是三角形的( )
| A. | 高 | B. | 角平分线 | C. | 中线 | D. | 外角平分线 |
17.已知一个二次函数y=ax2(a≠0)的图象经过(-2,6),则下列点中不在该函数的图象上的是( )
| A. | (2,6) | B. | (1,1.5) | C. | (-1,1.5) | D. | (2,8) |
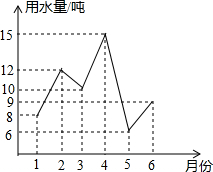 为了了解家里的用水情况,以便能更好的节约用水,小方把自己家1至6月份的用水量绘制成如图的折线图,那么小方家这6个月的月用水量最大是( )
为了了解家里的用水情况,以便能更好的节约用水,小方把自己家1至6月份的用水量绘制成如图的折线图,那么小方家这6个月的月用水量最大是( ) 我市出租车计费方法如图所示,x(千米)表示行驶里程,y(元)表示车费,请根据图象回答下列问题.
我市出租车计费方法如图所示,x(千米)表示行驶里程,y(元)表示车费,请根据图象回答下列问题.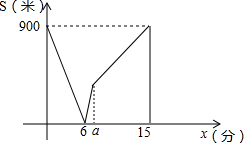 甲、乙两人在笔直的路上匀速行走,甲从A地步行前往B地,乙从B地步行前往A地,甲、乙两人同时出发,甲先到达B地后原地休息,甲、乙两人之间的距离S(米)与乙步行的时间t(分)之间的函数关系的图象如图所示,则a=10分钟.
甲、乙两人在笔直的路上匀速行走,甲从A地步行前往B地,乙从B地步行前往A地,甲、乙两人同时出发,甲先到达B地后原地休息,甲、乙两人之间的距离S(米)与乙步行的时间t(分)之间的函数关系的图象如图所示,则a=10分钟.