题目内容
12.对于二次函数y=$\frac{1}{2}$x2-3x+4,(1)配方成y=a(x-h)2+k的形式.
(2)求出它的图象的顶点坐标和对称轴.
(3)求出函数的最大或最小值.
分析 (1)直接利用配方法求出二次函数的顶点式即可;
(2)利用(1)中所求得出二次函数的顶点坐标和对称轴;
(3)利用(1)中所求得出二次函数的最值.
解答 解:(1)y=$\frac{1}{2}$x2-3x+4
=$\frac{1}{2}$(x2-6x)+4
=$\frac{1}{2}$[(x-3)2-9]+4
=$\frac{1}{2}$(x-3)2-$\frac{1}{2}$;
(2)由(1)得:图象的顶点坐标为:(3,-$\frac{1}{2}$),
对称轴为:直线x=3;
(3)∵a=$\frac{1}{2}$>0,
∴函数的最小值为:-$\frac{1}{2}$.
点评 此题主要考查了配方法求二次函数的最值与顶点坐标,正确进行配方是解题关键.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
20.能把一个三角形分成两个直角三角形的是三角形的( )
| A. | 高 | B. | 角平分线 | C. | 中线 | D. | 外角平分线 |
17.已知一个二次函数y=ax2(a≠0)的图象经过(-2,6),则下列点中不在该函数的图象上的是( )
| A. | (2,6) | B. | (1,1.5) | C. | (-1,1.5) | D. | (2,8) |
 我市出租车计费方法如图所示,x(千米)表示行驶里程,y(元)表示车费,请根据图象回答下列问题.
我市出租车计费方法如图所示,x(千米)表示行驶里程,y(元)表示车费,请根据图象回答下列问题. 如图,△ABC是等边三角形,点E是AB的中点,延长CB至D,使BD=$\frac{1}{2}$BC.
如图,△ABC是等边三角形,点E是AB的中点,延长CB至D,使BD=$\frac{1}{2}$BC.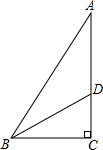 如图,在Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D.若BC=4cm,BD=5cm,则点D到AB的距离是3cm.
如图,在Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于点D.若BC=4cm,BD=5cm,则点D到AB的距离是3cm.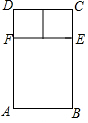 如图是一种窗框的设计示意图,矩形ABCD被分成上下两部分,上部的矩形CDFE由两个正方形组成,制作窗框的材料总长为6m.
如图是一种窗框的设计示意图,矩形ABCD被分成上下两部分,上部的矩形CDFE由两个正方形组成,制作窗框的材料总长为6m.