题目内容
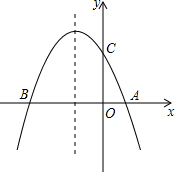 如图,抛物线y=-x2-2x+3于x轴交于A(1,0),B(-3,0)两点,交y轴于点C(0,3);在抛物线上是否存在点H,使得△BCH为直角三角形.
如图,抛物线y=-x2-2x+3于x轴交于A(1,0),B(-3,0)两点,交y轴于点C(0,3);在抛物线上是否存在点H,使得△BCH为直角三角形.考点:抛物线与x轴的交点
专题:
分析:可先求得顶点的坐标,再计算出DB、DC、BC,满足勾股定理的逆定理,可得出结论.
解答:解:∵抛物线y=-x2-2x+3=-(x+1)2+4,
∴抛物线顶点为D(-1,4),
又∵B(-3,0),C(0,3),
∴BD2=(-3+1)2+42=20,CD2=12+(3-4)2=2,BC=32+32=18,
∴BD2=CD2+BC2,
∴△BCD为直角三角形,
∴当H在顶点位置时,△BCH为直角三角形,
即在抛物线上存在使△BCH为直角三角形的点H.
∴抛物线顶点为D(-1,4),
又∵B(-3,0),C(0,3),
∴BD2=(-3+1)2+42=20,CD2=12+(3-4)2=2,BC=32+32=18,
∴BD2=CD2+BC2,
∴△BCD为直角三角形,
∴当H在顶点位置时,△BCH为直角三角形,
即在抛物线上存在使△BCH为直角三角形的点H.
点评:本题主要考查勾股定理的逆定理,利用条件表示出BD、CD、BC的长度是解题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 如图,点M(3,m)和点N(2,n)分别在抛物线y=
如图,点M(3,m)和点N(2,n)分别在抛物线y=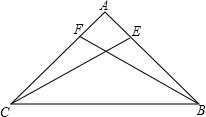 在△ABC中,BE=CF,∠CFB=∠BEC,那么AC=AB,你知道为什么吗?
在△ABC中,BE=CF,∠CFB=∠BEC,那么AC=AB,你知道为什么吗?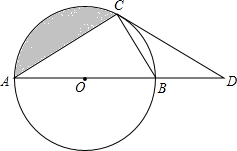 如图,AB是⊙O的直径,C为⊙O上一点,点D在AB的延长线上,∠DCB=∠A.
如图,AB是⊙O的直径,C为⊙O上一点,点D在AB的延长线上,∠DCB=∠A.  作图题:如图所示是每一个小方格都是边长为1的正方形网格,
作图题:如图所示是每一个小方格都是边长为1的正方形网格,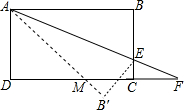 如图,在矩形ABCD中,AB=6cm,BC=3cm,点E是线段BC上的一个动点,连接AE并延长交DC延长线于点F,将△ABE沿直线AE翻折,点B落在B′处.线段AB′交CD于M点.当BE=2cm时,求DM.
如图,在矩形ABCD中,AB=6cm,BC=3cm,点E是线段BC上的一个动点,连接AE并延长交DC延长线于点F,将△ABE沿直线AE翻折,点B落在B′处.线段AB′交CD于M点.当BE=2cm时,求DM.