��Ŀ����
��CDE�͡�AOB����������ֱ�������Σ���CDE=��AOB=90�㣬DC=DE=1��OA=OB=a��a��1����
��1������CDE�Ķ���D���O�غϣ�����AE��BC��ȡ�߶�BC���е�M������OM��
����ͼ1����CD��DE�ֱ���OA��OB���غϣ����߶�OM��AE��������������ϵ����ֱ��д����Ľ����
����ͼ2����CD�ڡ�AOB�ڲ���������ͼ2�л�������ͼ�Σ��ж�OM��AE֮���������ϵ�Ƿ��б仯��д����IJ��룬������֤����
�۽���CDE�Ƶ�O����ת����д��OM��ȡֵ��Χ���ú�aʽ�ӱ�ʾ����
��2���Ƿ���ڱ߳����ġ�AOB��ʹ��CDE����������ֱ��ڡ�AOB���������ϣ������붥���غϣ���������ڣ����㻭����ʱ��ͼ�Σ�������߳�a��ֵ����������ڣ���˵�����ɣ�
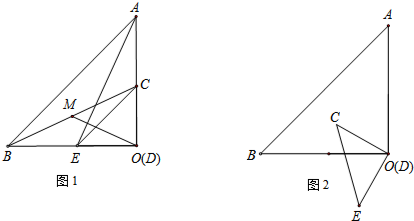
��1������CDE�Ķ���D���O�غϣ�����AE��BC��ȡ�߶�BC���е�M������OM��
����ͼ1����CD��DE�ֱ���OA��OB���غϣ����߶�OM��AE��������������ϵ����ֱ��д����Ľ����
����ͼ2����CD�ڡ�AOB�ڲ���������ͼ2�л�������ͼ�Σ��ж�OM��AE֮���������ϵ�Ƿ��б仯��д����IJ��룬������֤����
�۽���CDE�Ƶ�O����ת����д��OM��ȡֵ��Χ���ú�aʽ�ӱ�ʾ����
��2���Ƿ���ڱ߳����ġ�AOB��ʹ��CDE����������ֱ��ڡ�AOB���������ϣ������붥���غϣ���������ڣ����㻭����ʱ��ͼ�Σ�������߳�a��ֵ����������ڣ���˵�����ɣ�

���㣺���α任�ۺ���
ר�⣺
��������1�������á�CDE�ա�AOB�ó�BC=AE������ֱ��������б�ߵ����ߵ���б�ߵ�һ����⣮
���������ߣ����á�COF�ա�EOA����������λ�ߵó�OM=
AE��
�۷������������OC��OB�غ�ʱOM���OC��BO���ӳ�����ʱOM��С���ݴ����OM��ȡֵ��Χ��
��2�������������������D��б��AB��ʱ�����C����E�ֱ���OB��OA�ϣ���DM+OM��OF���ֱ�DZ�a�����ֵ��������D��ֱ�DZ�AO��ʱ����C����E�ֱ���OB��AB��ʱ������
��EHD�ա�DOC���ó�OD=EH����Rt��DHE�У����ù��ɶ���ED2=DH2+EH2���ó����̣��ɡ��ж���a�����ֵ��
���������ߣ����á�COF�ա�EOA����������λ�ߵó�OM=
| 1 |
| 2 |
�۷������������OC��OB�غ�ʱOM���OC��BO���ӳ�����ʱOM��С���ݴ����OM��ȡֵ��Χ��
��2�������������������D��б��AB��ʱ�����C����E�ֱ���OB��OA�ϣ���DM+OM��OF���ֱ�DZ�a�����ֵ��������D��ֱ�DZ�AO��ʱ����C����E�ֱ���OB��AB��ʱ������
��EHD�ա�DOC���ó�OD=EH����Rt��DHE�У����ù��ɶ���ED2=DH2+EH2���ó����̣��ɡ��ж���a�����ֵ��
����⣺��1���١ߡ�CDE�͡�AOB����������ֱ�������Σ�
��CD=ED��AO=B0����CDE=��AOB��
�ڡ�CDE�͡�AOB�У�
��
���CDE�ա�AOB��SAS����
��BC=AE
��MΪBC�е㣬
��OM=
BC��
��OM=
AE��
�ڲ��룺OM=
AE��
֤������ͼ2���ӳ�BO��F��ʹOF=OB������CF��

��MΪBC�е㣬
��OM=
CF��
�ߡ�CDE�͡�AOB����������ֱ�������Σ�
��CD=ED��AO=BO=OF����CDE=��AOB��
�ߡ�AOC+��COB=��BOE+��COB=90�㣬
���AOC=��BOE��
��FOC=��AOE��
�ڡ�COF�͡�EOA�У�
��
���COF�ա�EOA��
��CF=AE��
��OM=
AE��
�ۢ���ͼ3����OC��OB�غ�ʱ��OM���

OM=
+1=
��
����ͼ4����OC��BO���ӳ�����ʱ��OM��С��

OM=
-1=
��
����
��OM��
��
��2���⣺���ݡ�CDE�ĶԳ��ԣ�ֻ������������
����ͼ5��

������D��б��AB��ʱ�����C����E�ֱ���OB��OA�ϣ� ��OF��AB�ڵ�F��ȡCE���е�M������OD��MD��OM��
�ߡ�AOB�͡�CDE�ǵ���ֱ�������Σ���AOB=��CDE=90�㣬OA=OB=a��a��1����DC=DE=1��?????
��AB=
a��OF=
AB=
a��
��CE=
��DM=
CE=
��
��RT��COE��OM=
CE=
��
��RT��DOM��DM+OM��OD��
�֡�OD��OF��
��DM+OM��OF����
+
��
a��
��a��2��
��ֱ�DZ�a�����ֵΪ2��
����ͼ6��

������D��ֱ�DZ�AO��ʱ����C����E�ֱ���OB��AB�ϣ���EH��AO�ڵ�H��
�ߡ�AOB=��CDE=��DHE=90�㣬
�ߡ�HED+��EDH=��CDO+��EDH=90�㣬
���HED=��CDO��
��DC=DE��
�ڡ�EHD�͡�DOC�У�
���EHD�ա�DOC��AAS��
��OD=x��
��OD=EH=AH=x��DH=a-2x��
��Rt��DHE��ED2=DH2+EH2��
��1=x2+��a-2x��2��
�����ã�5x2-4ax+a2-1=0��
��x��ʵ����
���=��4a��2-4��5����a2-1��=20-4a2��0��
��a2��5��
��a2�����ֵΪ5��
��a�����ֵΪ
��?
����������a�����ֵΪ
��???
��CD=ED��AO=B0����CDE=��AOB��
�ڡ�CDE�͡�AOB�У�
|
���CDE�ա�AOB��SAS����
��BC=AE
��MΪBC�е㣬
��OM=
| 1 |
| 2 |
��OM=
| 1 |
| 2 |
�ڲ��룺OM=
| 1 |
| 2 |
֤������ͼ2���ӳ�BO��F��ʹOF=OB������CF��

��MΪBC�е㣬
��OM=
| 1 |
| 2 |
�ߡ�CDE�͡�AOB����������ֱ�������Σ�
��CD=ED��AO=BO=OF����CDE=��AOB��
�ߡ�AOC+��COB=��BOE+��COB=90�㣬
���AOC=��BOE��
��FOC=��AOE��
�ڡ�COF�͡�EOA�У�
|
���COF�ա�EOA��
��CF=AE��
��OM=
| 1 |
| 2 |
�ۢ���ͼ3����OC��OB�غ�ʱ��OM���

OM=
| a-1 |
| 2 |
| a+1 |
| 2 |
����ͼ4����OC��BO���ӳ�����ʱ��OM��С��

OM=
| a+1 |
| 2 |
| a-1 |
| 2 |
����
| a-1 |
| 2 |
| a+1 |
| 2 |
��2���⣺���ݡ�CDE�ĶԳ��ԣ�ֻ������������
����ͼ5��

������D��б��AB��ʱ�����C����E�ֱ���OB��OA�ϣ� ��OF��AB�ڵ�F��ȡCE���е�M������OD��MD��OM��
�ߡ�AOB�͡�CDE�ǵ���ֱ�������Σ���AOB=��CDE=90�㣬OA=OB=a��a��1����DC=DE=1��?????
��AB=
| 2 |
| 1 |
| 2 |
| ||
| 2 |
��CE=
| 2 |
| 1 |
| 2 |
| ||
| 2 |
��RT��COE��OM=
| 1 |
| 2 |
| ||
| 2 |
��RT��DOM��DM+OM��OD��
�֡�OD��OF��
��DM+OM��OF����
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
��a��2��
��ֱ�DZ�a�����ֵΪ2��
����ͼ6��

������D��ֱ�DZ�AO��ʱ����C����E�ֱ���OB��AB�ϣ���EH��AO�ڵ�H��
�ߡ�AOB=��CDE=��DHE=90�㣬
�ߡ�HED+��EDH=��CDO+��EDH=90�㣬
���HED=��CDO��
��DC=DE��
�ڡ�EHD�͡�DOC�У�
|
���EHD�ա�DOC��AAS��
��OD=x��
��OD=EH=AH=x��DH=a-2x��
��Rt��DHE��ED2=DH2+EH2��
��1=x2+��a-2x��2��
�����ã�5x2-4ax+a2-1=0��
��x��ʵ����
���=��4a��2-4��5����a2-1��=20-4a2��0��
��a2��5��
��a2�����ֵΪ5��
��a�����ֵΪ
| 5 |
����������a�����ֵΪ
| 5 |
������������Ҫ�����˼��α任�ۺ��⼰������ȫ�ȵ��ж������ʣ�����Ĺؼ�����ȡ���ֵʱ���������ε�λ�ý������۷ֱ���ֵ��

��ϰ��ϵ�д�
�����Ŀ
���е����У����˲���ȫ����飨�ղ飩��ʽ���ǣ�������
| A��ij������ˮ������ĵ��� |
| B��ijƷ���̻�����ȼ�Ű�ȫ����ĵ��� |
| C��һ���ƹ�ʹ�������ĵ��� |
| D���ԡ�����ʮ�š��ɴ����㲿���ϸ�����ĵ��� |
��������y=4x2����ƽ��1����λ��������ƽ��3����λ�����������ߵĽ���ʽΪ��������
| A��y=4��x+1��2+3 |
| B��y=4��x-1��2+3 |
| C��y=4��x+1��2-3 |
| D��y=4��x-1��2-3 |
 ��ͼ��ʾ�Ǵ�������
��ͼ��ʾ�Ǵ������� �ı�־ͼ���������̺������༸��֪ʶ������������������֤������֪����ͼ��BC��AD��BE��AF������DOB=135�㣬���A�Ķ����ǣ�������
�ı�־ͼ���������̺������༸��֪ʶ������������������֤������֪����ͼ��BC��AD��BE��AF������DOB=135�㣬���A�Ķ����ǣ�������| A��60�� | B��30�� |
| C��40�� | D��45�� |
��֪x=2��һԪ���η���x2+2ax+8=0��һ��������a��ֵΪ��������
| A��1 | B��-1 | C��3 | D��-3 |
 ��������ȫ��ͬ�ľ���ֽƬABCD��BFDE��ͼ���ã���֪AB=BF����֤���ı���BHDG�����Σ�
��������ȫ��ͬ�ľ���ֽƬABCD��BFDE��ͼ���ã���֪AB=BF����֤���ı���BHDG�����Σ�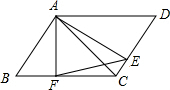 ��ͼ��ƽ���ı���ABCD�У�AF��BC�ڵ�F��AE��CD�ڵ�E������AC��FE����֤��AC•AF=EF•AB��
��ͼ��ƽ���ı���ABCD�У�AF��BC�ڵ�F��AE��CD�ڵ�E������AC��FE����֤��AC•AF=EF•AB��