题目内容
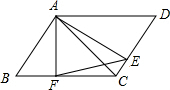如图，平行四边形ABCD中，AF⊥BC于点F，AE⊥CD于点E，连接AC、FE．求证：AC•AF=EF•AB．考点：相似三角形的判定与性质,平行四边形的性质
专题：证明题
分析：根据已知条件先证得△ABF∽△ADE，从而证得
=
，然后证得△ABC∽△FAE，即可求得．
| AF |
| AE |
| AB |
| BC |
解答：解；∵四边形ABCD是平行四边形，
∴AD=BC，∠B=∠D，
∵AF⊥BC，AE⊥CD，
∴∠AFB=∠AED=90°，
∴△ABF∽△ADE，
∴
=
，
∴
=
，
∵∠FAE+∠EAD=90°，∠D+∠EAD=90°，∠B=∠D，
∴∠B=∠FAE，
∴△ABC∽△FAE，
∴
=
，
即AC•AF=EF•AB．
∴AD=BC，∠B=∠D，
∵AF⊥BC，AE⊥CD，
∴∠AFB=∠AED=90°，
∴△ABF∽△ADE，
∴
| AF |
| AE |
| AB |
| AD |
∴
| AF |
| AE |
| AB |
| BC |
∵∠FAE+∠EAD=90°，∠D+∠EAD=90°，∠B=∠D，
∴∠B=∠FAE，
∴△ABC∽△FAE，
∴
| AB |
| AC |
| AF |
| EF |
即AC•AF=EF•AB．
点评：本题考查了平行四边形的性质，相似三角形的判定和性质，以及同角的余角相等等知识．
练习册系列答案
优学名师名题系列答案
相关题目
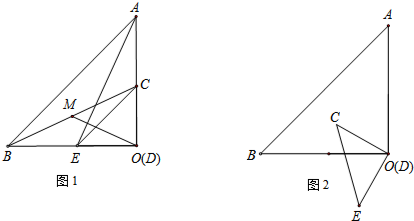
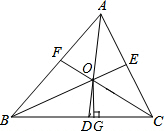如图，△ABC中，三条内角平分线AD、BE、CF相交于点O，OG⊥BC于点G．
如图，已知DE∥AB，BD平∠ABC分，∠1=∠2，求证：EF平分∠CED．