题目内容
 把两个完全相同的矩形纸片ABCD,BFDE如图放置,已知AB=BF,求证:四边形BHDG是菱形.
把两个完全相同的矩形纸片ABCD,BFDE如图放置,已知AB=BF,求证:四边形BHDG是菱形.考点:菱形的判定
专题:证明题
分析:易证四边形BHDG是平行四边形;根据AB=BF,运用AAS可证明Rt△ABG≌Rt△FBH,得BG=BH.根据有一邻边相等的平行四边形是菱形得证.
解答:证明:∵两个完全相同的矩形纸片ABCD、BFDE,根据矩形的对边平行,
∴BA∥CD,BE∥DF,
∴四边形BHDG是平行四边形,
∵∠ABG+∠GBH=90°,∠GBH+∠FBH=90°,
∴∠ABG=∠FBH.
在△ABG和△FBH中,
∴△ABG≌△FBH,(ASA).
∴BG=BH,
∴四边形BHDG是菱形.
∴BA∥CD,BE∥DF,
∴四边形BHDG是平行四边形,
∵∠ABG+∠GBH=90°,∠GBH+∠FBH=90°,
∴∠ABG=∠FBH.
在△ABG和△FBH中,
|
∴△ABG≌△FBH,(ASA).
∴BG=BH,
∴四边形BHDG是菱形.
点评:本题考查了菱形的判断,菱形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:①定义;②四边相等;③对角线互相垂直平分.具体选择哪种方法需要根据已知条件来确定.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若关于x的方程3x2+mx+2m-6=0的一个根是0,则m的值为( )
| A、6 | B、3 | C、2 | D、1 |
 如图,过点F(2,3)分别作x轴,y轴的垂线,垂足为C,D.FC,FD分别交反比例函数Y=
如图,过点F(2,3)分别作x轴,y轴的垂线,垂足为C,D.FC,FD分别交反比例函数Y=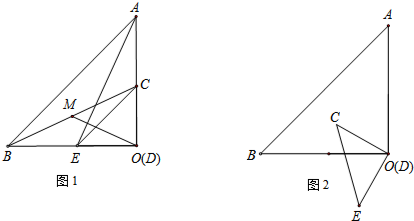
 在如图的四边形ABCD中,若∠A=90°,∠ADB=30°,AB=3,BC=10,CD=8,试求四边形ABCD的面积.
在如图的四边形ABCD中,若∠A=90°,∠ADB=30°,AB=3,BC=10,CD=8,试求四边形ABCD的面积.
 如图,平行四边形ABCD中,对角线AC、BD相交于点O,若E、F是AC上两动点,分别从A、C两点以相同的速度1cm/s向C、A运动.
如图,平行四边形ABCD中,对角线AC、BD相交于点O,若E、F是AC上两动点,分别从A、C两点以相同的速度1cm/s向C、A运动.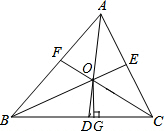 如图,△ABC中,三条内角平分线AD、BE、CF相交于点O,OG⊥BC于点G.
如图,△ABC中,三条内角平分线AD、BE、CF相交于点O,OG⊥BC于点G.