题目内容
3.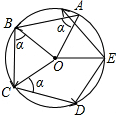 如图,小明从一个圆形场地边沿点A出发,按逆时针方向运动,先沿∠OAB=α的方向走到场地边沿的点B,再沿∠OBC=α的方向走到场地边沿的点C…,照此继续行走并依字母顺序标记,结果点F首次越过了点A并恰好处于$\widehat{AB}$的中点.如果小明希望下一次行走路线正好是⊙O的内接正九边形,那么他应将最初的角α增大或减小多少度?
如图,小明从一个圆形场地边沿点A出发,按逆时针方向运动,先沿∠OAB=α的方向走到场地边沿的点B,再沿∠OBC=α的方向走到场地边沿的点C…,照此继续行走并依字母顺序标记,结果点F首次越过了点A并恰好处于$\widehat{AB}$的中点.如果小明希望下一次行走路线正好是⊙O的内接正九边形,那么他应将最初的角α增大或减小多少度?
分析 根据题意求出α的度数,然后求出小明下一次行走路线正好是⊙O的内接正九边形的角的度数,求差即可.
解答 解:由题意可知,小明每一次沿∠OAB=α的方向走,则每一次转过的圆心角是180°-2α,
运动到点F一共运动了5次,多转了$\frac{1}{2}$(180°-2α)=90°-α,
则5(180°-2α)=360°+90°-α,
解得α=50°,
若构成正九边形,则运动了九次,
设沿β的度数转动,9(180°-2β)=360°,
β=70°,
β-α=70°-50°=20°.
答:他应将最初的角α增大20度.
点评 本题考查的是正多边形和圆的知识,掌握正多边形的中心角的计算方法是解题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
13. 如图,数轴上表示$\sqrt{3}$,2的对应点分别为A、B,点B关于点A的对称点为C,则点C表示的实数为( )
如图,数轴上表示$\sqrt{3}$,2的对应点分别为A、B,点B关于点A的对称点为C,则点C表示的实数为( )
 如图,数轴上表示$\sqrt{3}$,2的对应点分别为A、B,点B关于点A的对称点为C,则点C表示的实数为( )
如图,数轴上表示$\sqrt{3}$,2的对应点分别为A、B,点B关于点A的对称点为C,则点C表示的实数为( )| A. | $\sqrt{3}$-2 | B. | 2-$\sqrt{3}$ | C. | $\sqrt{3}$-1 | D. | $2\sqrt{3}$-2 |
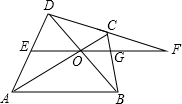 如图,四边形ABCD中,AC、BD交于O,过O作直线EF∥AB,交AD、BC于E,G,交DC延长线于F,求证:FO2=FG•FE.
如图,四边形ABCD中,AC、BD交于O,过O作直线EF∥AB,交AD、BC于E,G,交DC延长线于F,求证:FO2=FG•FE.
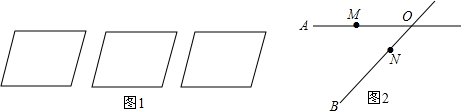
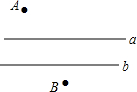 如图,幸福小区A和超市B位于公路的两侧,现要在公路上建一座天桥,天桥建在何处可使小区A的人到超市B购物最近?(假定公路的两边是平行的直线,天桥与公路垂直)
如图,幸福小区A和超市B位于公路的两侧,现要在公路上建一座天桥,天桥建在何处可使小区A的人到超市B购物最近?(假定公路的两边是平行的直线,天桥与公路垂直)