题目内容
18.已知a<0,关于x的方程$\frac{1}{x}$+$\frac{1}{x+a}$+$\frac{1}{x+{a}^{2}}$=0,求证:(1)方程必有两个异号实根;
(2)正根必小于-$\frac{2}{3}$a,负根必大于-$\frac{2}{3}$a2.
分析 (1)方程去分母整理得到关于x的一元二次方程,根据a<0,判断根的判别式大于0,且两根之积小于0,即可得到方程必有两个异号实根;
(2)设方程的两根为x1,x2,且x1>0>x2,利用求根公式表示出两根,利用不等式的性质化简即可得证.
解答 证明:(1)方程去分母得:3x2+(2a2+2a)x+a3=0,
设方程的两根为x1,x2,
∵a<0,∴-a3>0,a4>0,a2>0,即a4-a3+a2>0,
∴△=(2a2+2a)2-12a3=4a4+8a3+4a2-12a3=4a4-4a3+4a2=4(a4-a3+a2)>0,且x1x2=$\frac{{a}^{3}}{3}$<0,
则方程必有两个异号实根;
(2)设方程的两根为x1,x2,且x1>0>x2,
∵x=$\frac{-2{a}^{2}-2a+2\sqrt{{a}^{4}-{a}^{3}+{a}^{2}}}{6}$=$\frac{-{a}^{2}-a±a\sqrt{{a}^{2}-a+1}}{3}$,
∴x1=$\frac{-{a}^{2}-a-a\sqrt{{a}^{2}-a+1}}{3}$<$\frac{-{a}^{2}-a-a\sqrt{{a}^{2}-2a+1}}{3}$=$\frac{-{a}^{2}-a-a(1-a)}{3}$=-$\frac{2}{3}$a,
x2=$\frac{-{a}^{2}-a+a\sqrt{{a}^{2}-a+1}}{3}$>$\frac{-{a}^{2}-a+a\sqrt{{a}^{2}-2a+1}}{3}$=$\frac{-{a}^{2}-a+a(1-a)}{3}$=-$\frac{2}{3}$a2,
则正根必小于-$\frac{2}{3}$a,负根必大于-$\frac{2}{3}$a2.
点评 此题考查了分式方程的解,一元二次方程根的判别式,根与系数得关系,以及不等式的性质,熟练掌握运算法则是解本题的关键.

 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案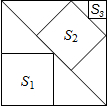 如图,边长为18的大正方形中有三个小正方形,若三个小正方形的面积分别为S1、S2、S3,则S1+S2+S3的值162.
如图,边长为18的大正方形中有三个小正方形,若三个小正方形的面积分别为S1、S2、S3,则S1+S2+S3的值162.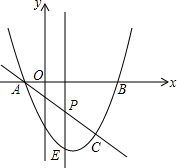 如图,抛物线y=x2-2x-3与x轴交A,B两点(A点在B点左侧),直线l与抛物线交于A,C两点,其中C点的横坐标为2.
如图,抛物线y=x2-2x-3与x轴交A,B两点(A点在B点左侧),直线l与抛物线交于A,C两点,其中C点的横坐标为2.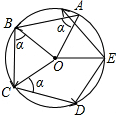 如图,小明从一个圆形场地边沿点A出发,按逆时针方向运动,先沿∠OAB=α的方向走到场地边沿的点B,再沿∠OBC=α的方向走到场地边沿的点C…,照此继续行走并依字母顺序标记,结果点F首次越过了点A并恰好处于$\widehat{AB}$的中点.如果小明希望下一次行走路线正好是⊙O的内接正九边形,那么他应将最初的角α增大或减小多少度?
如图,小明从一个圆形场地边沿点A出发,按逆时针方向运动,先沿∠OAB=α的方向走到场地边沿的点B,再沿∠OBC=α的方向走到场地边沿的点C…,照此继续行走并依字母顺序标记,结果点F首次越过了点A并恰好处于$\widehat{AB}$的中点.如果小明希望下一次行走路线正好是⊙O的内接正九边形,那么他应将最初的角α增大或减小多少度?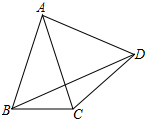 如图,△ABC中,AB=AC,∠BAC=40°,边AB绕点A逆时针旋转m°,(0<m<360)得到线段AD,连接BD、DC.若△BDC为等腰三角形,则m所有可能的取值是20°,80°,200°,320°.
如图,△ABC中,AB=AC,∠BAC=40°,边AB绕点A逆时针旋转m°,(0<m<360)得到线段AD,连接BD、DC.若△BDC为等腰三角形,则m所有可能的取值是20°,80°,200°,320°.