题目内容
16.平面直角坐标系中,若一动点P(x,y)到点F(0,1)的距离与点P到直线y=-1的距离相等,满足要求的动点P在某一条抛物线上,则此抛物线的解析式为y=$\frac{1}{4}$x2.分析 先利用两点间的距离公式得到P(x,y)到点F(0,1)的距离为$\sqrt{{x}^{2}+(y-1)^{2}}$,点P到直线y=-1的距离为y+1,x2+(y-1)2=(y+1)2,然后用x表示y即可.
解答 解:P(x,y)到点F(0,1)的距离为$\sqrt{{x}^{2}+(y-1)^{2}}$,点P到直线y=-1的距离为y+1,
则$\sqrt{{x}^{2}+(y-1)^{2}}$=y+1,
即x2+(y-1)2=(y+1)2,
整理得y=$\frac{1}{4}$x2,
即动点P在抛物线y=$\frac{1}{4}$x2上.
故答案为y=$\frac{1}{4}$x2.
点评 本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.也考查了两点间的距离公式.

练习册系列答案
相关题目
1.小磊解题时,将式子(-$\frac{1}{6}$)+(-7)+$\frac{5}{6}$+(-4)先变成[(-$\frac{1}{6}$)+$\frac{5}{6}$]+[(-7)+(-4)]再计算结果,则小磊运用了( )
| A. | 加法交换律 | B. | 加法交换律和加法结合律 | ||
| C. | 加法结合律 | D. | 无法判断 |
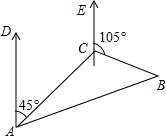 某货船在索马里海域航行中遭遇海盗袭击,发出呼救信号,我海军护航舰在A处获悉后,立即测出该船在方位角45°,距离10海里的C处,并测得该船正沿方位角105°的方向,以每小时10海里的速度向前行驶,我海军护航舰立即以每小时10$\sqrt{3}$海里的速度前去营救,求护航舰的舰向和靠近货船所需的时间.
某货船在索马里海域航行中遭遇海盗袭击,发出呼救信号,我海军护航舰在A处获悉后,立即测出该船在方位角45°,距离10海里的C处,并测得该船正沿方位角105°的方向,以每小时10海里的速度向前行驶,我海军护航舰立即以每小时10$\sqrt{3}$海里的速度前去营救,求护航舰的舰向和靠近货船所需的时间. 已知,如图,AB,CD相交于0,且∠C=∠D,OC=OD,求证:△ACO≌△BDO.
已知,如图,AB,CD相交于0,且∠C=∠D,OC=OD,求证:△ACO≌△BDO.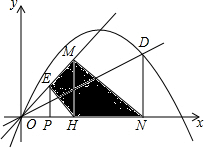 如图,在平面直角坐标系中,等腰直角三角形OMN的斜边ON在x轴上,顶点M的坐标为(3,3),MH为斜边上的高.过N点垂直于x轴的直线与抛物线y=-$\frac{1}{4}{x}^{2}+nx$交于点D,直线OD的解析式为y=$\frac{1}{2}x$.点P(x,0)是x轴上一动点,过点P作y轴的平行线,交射线OM于点E.
如图,在平面直角坐标系中,等腰直角三角形OMN的斜边ON在x轴上,顶点M的坐标为(3,3),MH为斜边上的高.过N点垂直于x轴的直线与抛物线y=-$\frac{1}{4}{x}^{2}+nx$交于点D,直线OD的解析式为y=$\frac{1}{2}x$.点P(x,0)是x轴上一动点,过点P作y轴的平行线,交射线OM于点E.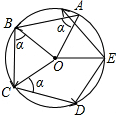 如图,小明从一个圆形场地边沿点A出发,按逆时针方向运动,先沿∠OAB=α的方向走到场地边沿的点B,再沿∠OBC=α的方向走到场地边沿的点C…,照此继续行走并依字母顺序标记,结果点F首次越过了点A并恰好处于$\widehat{AB}$的中点.如果小明希望下一次行走路线正好是⊙O的内接正九边形,那么他应将最初的角α增大或减小多少度?
如图,小明从一个圆形场地边沿点A出发,按逆时针方向运动,先沿∠OAB=α的方向走到场地边沿的点B,再沿∠OBC=α的方向走到场地边沿的点C…,照此继续行走并依字母顺序标记,结果点F首次越过了点A并恰好处于$\widehat{AB}$的中点.如果小明希望下一次行走路线正好是⊙O的内接正九边形,那么他应将最初的角α增大或减小多少度?