��Ŀ����
16��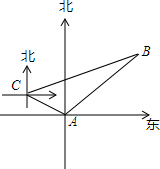 ��ͼ���ס�����ֻ���̴�ͬʱ��A�۳������㣬�״���ÿСʱ$15\sqrt{2}$ǧ���ٶ��ر�ƫ��60�㷽��ǰ�����Ҵ���ÿСʱ15ǧ���ٶ��ض�������ǰ�����״�����2Сʱ����C������ʱ�״�������߶����Ҵ��ϣ����Ǽ״��ӿ��ٶȣ����٣��ر�ƫ��75��ķ����ϣ����������B��������
��ͼ���ס�����ֻ���̴�ͬʱ��A�۳������㣬�״���ÿСʱ$15\sqrt{2}$ǧ���ٶ��ر�ƫ��60�㷽��ǰ�����Ҵ���ÿСʱ15ǧ���ٶ��ض�������ǰ�����״�����2Сʱ����C������ʱ�״�������߶����Ҵ��ϣ����Ǽ״��ӿ��ٶȣ����٣��ر�ƫ��75��ķ����ϣ����������B����������1���״���C�������Ҵ����˶���ʱ�䣿
��2����״��ӿ��ٶȺ����Ҵ�ʱ���ٶȣ�������������ţ�
���� ��1������A��AD��BC��D������������Ǻ�����ϵ�ó�AC�ij��������ó�AB�ij����ɵó��𰸣�
��2�����ã�1�����BD�ij����������ٶ�=$\frac{·��}{ʱ��}$������𰸼��ɣ�
���  �⣺��1������A��AD��BC��D��
�⣺��1������A��AD��BC��D��
������ã�
��B=30�㣬��BAC=105�㣬
���BCA=45�㣬AC=30$\sqrt{2}$ǧ�ף�
��Rt��ADC�У�CD=AD=AC��cos45��=30��ǧ�ף���
��Rt��ABD�У�AB=2AD=60ǧ�ף�t=$\frac{60}{15}$=4��ʱ����
4-2=2��ʱ����
�𣺼״���C�������Ҵ�����2Сʱ��
��2���ɣ�1��֪��BD=AB•cos30��=30$\sqrt{3}$ǧ�ף�
��BC=30+30$\sqrt{3}$��ǧ�ף���
v=��30+30$\sqrt{3}$����2=��15+15$\sqrt{3}$��ǧ��/ʱ��
�𣺼״��ӿ��ٶȺ����Ҵ�ʱ���ٶ�Ϊ����15+15$\sqrt{3}$��ǧ��/ʱ��
���� ������Ҫ�����˽�ֱ�������ε�Ӧ�ã���������ó�AC��CD�ij��ǽ���ؼ���

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
4����������$y=-\frac{1}{3}{��x-2��^2}$ƽ�ƺ�õ�$y=-\frac{1}{3}{x^2}$��ƽ�Ƶķ��������ǣ�������
| A�� | ��x������ƽ��2����λ | B�� | ��x������ƽ��2����λ | ||
| C�� | ��y������ƽ��2����λ | D�� | ��y������ƽ��2����λ |
1�������������������
��1��a10��a2=a5 ��2��a5•a��a=a5 ��3����-a��5�£�-a��3=-a2 ��4��30=3��
��1��a10��a2=a5 ��2��a5•a��a=a5 ��3����-a��5�£�-a��3=-a2 ��4��30=3��
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
5��С����������3�������⣺��-2-2=0����-2-|-2|=-4����-2+3=1������������һ�£���һ�������ˣ�������
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 0�� |
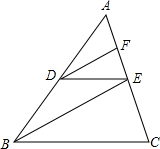 ��֪�ڡ�ABC�У���D�ڱ�AB�ϣ���E��F�ڱ�AC�ϣ���DE��BC��DF��BE����֤��$\frac{AF}{AE}$=$\frac{AE}{AC}$��
��֪�ڡ�ABC�У���D�ڱ�AB�ϣ���E��F�ڱ�AC�ϣ���DE��BC��DF��BE����֤��$\frac{AF}{AE}$=$\frac{AE}{AC}$�� ��֪����ͼ���ڡ�ABC�У�BD�ǡ�ABC��ƽ���ߣ�����D��DE��CB����AB�ڵ�E��$\frac{AD}{DC}=\frac{1}{3}$��DE=6��
��֪����ͼ���ڡ�ABC�У�BD�ǡ�ABC��ƽ���ߣ�����D��DE��CB����AB�ڵ�E��$\frac{AD}{DC}=\frac{1}{3}$��DE=6��