题目内容
4．把抛物线$y=-\frac{1}{3}{（x-2）^2}$平移后得到$y=-\frac{1}{3}{x^2}$，平移的方法可以是（ ）| A． | 沿x轴向左平移2个单位 | B． | 沿x轴向右平移2个单位 | ||
| C． | 沿y轴向上平移2个单位 | D． | 沿y轴向下平移2个单位 |
分析 原抛物线顶点坐标为（2，0），平移后抛物线顶点坐标为（0，0），由此确定平移规律．
解答 解：∵抛物线$y=-\frac{1}{3}{（x-2）^2}$的顶点坐标为（2，0），抛物线$y=-\frac{1}{3}{x^2}$的顶点坐标为（0，0），
∴平移的方法可以是：x轴向左平移2个单位．
故选A．
点评 本题考查了二次函数图象与几何变换．关键是将抛物线的平移问题转化为顶点的平移，寻找平移方法．
练习册系列答案
相关题目
在数轴上表示有理数a，b，c的对应点A，B，C，如图，试化简下列式子：|a-b|+|c-a|-|a+b|-|b-c|．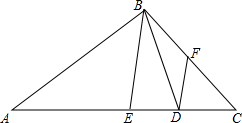
如图，△ABC∽△BDC，E，F分别为AC，BC的中点，已知AC=6，BC=4，BE=3，求DF的长．
19．下面4个汽车标志图案中，不是轴对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
如图，正方形ABCD中，E是CD中点，$FC=\frac{1}{4}BC$，则tan∠EAF=$\frac{1}{2}$．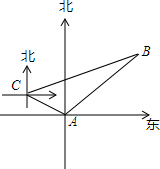
如图，甲、乙两只捕捞船同时从A港出海捕鱼，甲船以每小时$15\sqrt{2}$千米的速度沿北偏西60°方向前进，乙船以每小时15千米的速度沿东北方向前进，甲船航行2小时到达C处，此时甲船发现渔具丢在乙船上，于是甲船加快速度（匀速）沿北偏东75°的方向追赶，结果两船在B处相遇．