题目内容
11. 已知:如图,在△ABC中,BD是∠ABC的平分线,过点D作DE∥CB,交AB于点E,$\frac{AD}{DC}=\frac{1}{3}$,DE=6.
已知:如图,在△ABC中,BD是∠ABC的平分线,过点D作DE∥CB,交AB于点E,$\frac{AD}{DC}=\frac{1}{3}$,DE=6.(1)求AB的长;
(2)求$\frac{{{S_{△ADE}}}}{{{S_{△BCD}}}}$.
分析 (1)由∠ABD=∠CBD,DE∥BC 可推得∠EDB=∠CBD,进而推出∠ABD=∠EDB,由此可得BE=DE=6,由DE∥BC 可得$\frac{AE}{EB}=\frac{AD}{DC}=\frac{1}{3}$,进而证得AE=2,于是可得结论;
(2)△ADE看成以DE为底,高为h1,△BCD看成以BC为底,高为h2,由平行线分线段成比例定理和相似三角形的性质可得$\frac{{h}_{1}}{{h}_{2}}$=$\frac{AD}{DE}=\frac{1}{3}$,$\frac{DE}{BC}=\frac{1}{4}$,进而证得结论.
解答  解:(1)BD平∠ABC,
解:(1)BD平∠ABC,
∴∠ABD=∠CBD,
∵DE∥BC,
∴∠EDB=∠CBD,
∴∠ABD=∠EDB,
∴BE=DE=6,
∵DE∥BC,
∴$\frac{AE}{EB}=\frac{AD}{DC}=\frac{1}{3}$,
∴$\frac{AE}{6}=\frac{1}{3}$,
∴AE=2,
∴AB=AE+BE=8;
(2)△ADE看成以DE为底,高为h1,△BCD看成以BC为底,高为h2,
∵DE∥CB,
∴△AED~△ABC,
∴$\frac{{h}_{1}}{{h}_{2}}$=$\frac{AD}{DE}=\frac{1}{3}$,$\frac{DE}{BC}=\frac{1}{4}$,
∴$\frac{{S}_{△ADE}}{{S}_{△BCD}}=\frac{\frac{1}{2}DE•{h}_{1}}{\frac{1}{2}BC•{h}_{2}}=\frac{1}{12}$.
点评 本题主要考查了等腰三角形的性质,平行线分线段成比例定理和相似三角形的性质,三角形的面积等知识,熟练应用平行线分线段成比例定理和相似三角形的性质是解决问题的关键.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案 我校七年级学生总人数为700,其男女生所占比例如图所示,则该校七年级男生人数为( )
我校七年级学生总人数为700,其男女生所占比例如图所示,则该校七年级男生人数为( )| A. | 48 | B. | 52 | C. | 336 | D. | 364 |
| A. |  | B. |  | C. |  | D. |  |
| A. | ∠D=40°,∠E=80°,∠A=60°,∠B=80° | |
| B. | ∠A=∠D,AB:AC=DF:EF | |
| C. | ∠B=∠E=90°,BC:EF=AC:DF | |
| D. | AB=1,BC=2,CA=1.5,DE=6,EF=4,FD=8 |
| A. | x≥0 | B. | x≥3 | C. | 0≤x≤3 | D. | x为任意实数 |




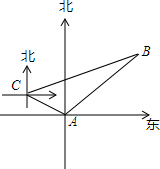 如图,甲、乙两只捕捞船同时从A港出海捕鱼,甲船以每小时$15\sqrt{2}$千米的速度沿北偏西60°方向前进,乙船以每小时15千米的速度沿东北方向前进,甲船航行2小时到达C处,此时甲船发现渔具丢在乙船上,于是甲船加快速度(匀速)沿北偏东75°的方向追赶,结果两船在B处相遇.
如图,甲、乙两只捕捞船同时从A港出海捕鱼,甲船以每小时$15\sqrt{2}$千米的速度沿北偏西60°方向前进,乙船以每小时15千米的速度沿东北方向前进,甲船航行2小时到达C处,此时甲船发现渔具丢在乙船上,于是甲船加快速度(匀速)沿北偏东75°的方向追赶,结果两船在B处相遇.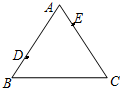 如图△ABC中,AB=8,AC=6,如果动点D以每秒2个单位长的速度,从点B出发沿BA方向向点A运动,同时点E以每秒1个单位的速度从点A出发沿AC方向向点C运动,设运动时间为t(单位:秒),问t为何值时△ADE与△ABC相似.
如图△ABC中,AB=8,AC=6,如果动点D以每秒2个单位长的速度,从点B出发沿BA方向向点A运动,同时点E以每秒1个单位的速度从点A出发沿AC方向向点C运动,设运动时间为t(单位:秒),问t为何值时△ADE与△ABC相似.