题目内容
19.下列各数 $\frac{22}{7}$,-0.333…,3.14,$\frac{π}{2}$,0.1010010001…中,无理数的个数有( )个.| A. | .1 个 | B. | 2 个 | C. | .3 个 | D. | .4 个 |
分析 根据无理数的概念,找出五个数中是无理数的数,此题得解.
解答 解:∵在 $\frac{22}{7}$、-0.333…、3.14、$\frac{π}{2}$、0.1010010001…中,无限循环小数有:$\frac{22}{7}$、-0.333…;有限小数有:3.14;无限不循环小数有:$\frac{π}{2}$、0.1010010001…,
∴$\frac{π}{2}$和01010010001…为无理数.
故选B.
点评 本题考查了无理数,牢记无理数的概念是解题的关键.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
14.下列计算中,不正确的是( )
| A. | 2$\sqrt{3}$+(-2$\sqrt{3}$)=0 | B. | ($\sqrt{3}$+$\sqrt{7}$)•($\sqrt{3}$-$\sqrt{7}$)=-4 | C. | ($\sqrt{10}$)3•$\sqrt{10}$=100 | D. | ($\sqrt{2a}$+$\sqrt{b}$)($\sqrt{2a}$+$\sqrt{b}$)=2a+b |
8.下列说法错误的是( )
| A. | 实数与数轴上的点一一对应 | |
| B. | 无限小数未必是无理数,但无理数一定是无限小数 | |
| C. | 分数总是可以化成小数,但小数未必能转化为分数 | |
| D. | 有理数都可以表示成有限小数或无限循环小数 |
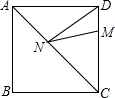 如图,正方形ABCD的边长为16,M在DC上,且DM=4,N是AC上的一动点,则DN+MN的最小值是20.
如图,正方形ABCD的边长为16,M在DC上,且DM=4,N是AC上的一动点,则DN+MN的最小值是20. 一个正三棱柱的三视图如图所示,若这个正三棱柱的侧面积为12$\sqrt{3}$,则a的值为$\sqrt{3}$.
一个正三棱柱的三视图如图所示,若这个正三棱柱的侧面积为12$\sqrt{3}$,则a的值为$\sqrt{3}$.