题目内容
学校举办一年一届的科技文化艺术节活动,需制作一块活动展板,请来两名工人.已知师傅单独完成需4天,徒弟单独完成需6天.
(1)两个人合作需要 天完成;
(2)现由徒弟先做1天,再两个合作,问:还需几天可以完成这项工作?
(1)两个人合作需要
(2)现由徒弟先做1天,再两个合作,问:还需几天可以完成这项工作?
考点:一元一次方程的应用
专题:
分析:(1)完成工作的工作量为1,根据工作时间=工作总量÷工作效率和,列式即可求解.
(2)设徒弟先做1天,再两人合作还需x天完成,根据等量关系:完成工作的工作总量为1,列出方程即可求解.
(2)设徒弟先做1天,再两人合作还需x天完成,根据等量关系:完成工作的工作总量为1,列出方程即可求解.
解答:解:(1)1÷(
+
)
=1÷
=2.4(天).
答:两个人合作需要2.4天完成;
(2)设还需x天可以完成这项工作,由题意可得:
+
=1,
解得:x=2.
答:还需2天可以完成这项工作.
故答案为:2.4.
| 1 |
| 4 |
| 1 |
| 6 |
=1÷
| 5 |
| 12 |
=2.4(天).
答:两个人合作需要2.4天完成;
(2)设还需x天可以完成这项工作,由题意可得:
| x+1 |
| 6 |
| x |
| 4 |
解得:x=2.
答:还需2天可以完成这项工作.
故答案为:2.4.
点评:考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
相关题目
若M(-4,y1)、N(-2,y2)、H(2,y3)三点都在反比例函数y=
(k>0)的图象上,则y1、y2、y3的大小关系为( )
| k |
| x |
| A、y1<y2<y3 |
| B、y2<y1<y3 |
| C、y3<y2<y1 |
| D、y3<y1<y2 |
已知直角坐标系中,点P(x,y)满足
+(y+3)2=0,则点P坐标为( )
| x2-4 |
| A、(2,-3) |
| B、(-2,3) |
| C、(2,3) |
| D、(2,-3)或(-2,-3) |

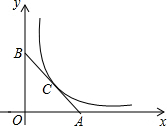 如图,在平面直角坐标系中,点A(4,0)、B(0,4),连接AB,反比例函数y=
如图,在平面直角坐标系中,点A(4,0)、B(0,4),连接AB,反比例函数y=