题目内容
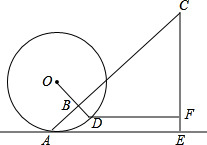 滚铁环是一项老少皆宜的体育运动,如图,铁环⊙O的半径为34cm,且与地面AE切于点A.钩BD的长为4cm,柄BC的长为69cm,且BD⊥BC于点B.某一时刻,DB的延长线经过圆心O,且CB的延长线经过切点A,这时,握手点C离地面的高度CE=
滚铁环是一项老少皆宜的体育运动,如图,铁环⊙O的半径为34cm,且与地面AE切于点A.钩BD的长为4cm,柄BC的长为69cm,且BD⊥BC于点B.某一时刻,DB的延长线经过圆心O,且CB的延长线经过切点A,这时,握手点C离地面的高度CE=考点:切线的性质
专题:
分析:连接OA,延长FD交OA于G,根据切线的性质求得OA⊥AE,进而求得∠AOB=∠CAE,从而求得△OAB∽△ACE,根据勾股定理求得AB,再根据相似三角形对应边成比例求得CE,根据AAS求得△OAB≌△ODG,得出GD=AB=16cm,根据勾股定理求得AE,从而求得GF,即可求得DF的长.
解答: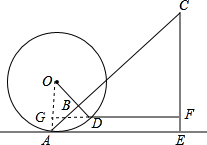 解:连接OA,延长FD交OA于G,
解:连接OA,延长FD交OA于G,
∵铁环⊙O与地面AE切于点A.
∴OA⊥AE,
∴∠OAB+∠CAE=90°,
∵BD⊥BC,
∴∠OAB+∠AOB=90°,
∴∠AOB=∠CAE,
∵∠ABO=∠AEC=90°,
∴△OAB∽△ACE,
∴
=
,
∵OB=34-4=30cm,OA=34cm,
∴AB=
=16cm,
∴AC=16+69=85cm,
∴
=
,解得,CE=40cm,
在△OAB和△ODG中,
,
∴△OAB≌△ODG(AAS),
∴DG=AB=16cm,
∵GF=AE=
=
=75cm,
∴DF=GF-GD=75-16=59cm.
故答案为40,59.
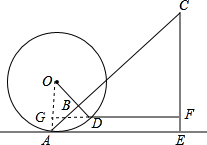 解:连接OA,延长FD交OA于G,
解:连接OA,延长FD交OA于G,∵铁环⊙O与地面AE切于点A.
∴OA⊥AE,
∴∠OAB+∠CAE=90°,
∵BD⊥BC,
∴∠OAB+∠AOB=90°,
∴∠AOB=∠CAE,
∵∠ABO=∠AEC=90°,
∴△OAB∽△ACE,
∴
| AO |
| AC |
| AB |
| CE |
∵OB=34-4=30cm,OA=34cm,
∴AB=
| OA2-OB2 |
∴AC=16+69=85cm,
∴
| 34 |
| 85 |
| 16 |
| CE |
在△OAB和△ODG中,
|
∴△OAB≌△ODG(AAS),
∴DG=AB=16cm,
∵GF=AE=
| AC2-CE2 |
| 852-402 |
∴DF=GF-GD=75-16=59cm.
故答案为40,59.
点评:本题考查了切线的性质,勾股定理的应用,三角形的内角和定理的应用以及三角形全等的判定和性质,解此题的关键是求出∠AOB=∠CAE,注意:圆的切线垂直于过切点的半径.

练习册系列答案
相关题目
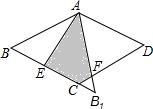 如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB1E,则△AB1E与四边形AECD重叠部分的面积为( )
如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB1E,则△AB1E与四边形AECD重叠部分的面积为( )| A、0.7 | ||||
| B、0.9 | ||||
C、2
| ||||
D、
|
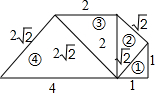 如图,第①个等腰直角三角形斜边为
如图,第①个等腰直角三角形斜边为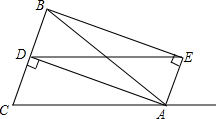 如图,△ABC中,AB=AC,AD⊥BC于点D,AE是∠BAC外角平分线,BE⊥AE,连接DE.
如图,△ABC中,AB=AC,AD⊥BC于点D,AE是∠BAC外角平分线,BE⊥AE,连接DE. 如图,一副三角板(直角顶点重合)摆放在桌面上,若∠AOD=150°,则∠BOC等于
如图,一副三角板(直角顶点重合)摆放在桌面上,若∠AOD=150°,则∠BOC等于