题目内容
已知在边长为4的正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD上一点,若△ADQ与△PCQ相似,求DQ的长.
考点:正方形的性质,相似三角形的性质
专题:
分析:运用分类讨论的数学思想,按△ADQ∽△PCQ,或△ADQ∽△QCP两种情况,列出比例式逐一解析,即可解决问题.
解答: 解:如图,∵四边形ABCD为正方形,
解:如图,∵四边形ABCD为正方形,
且BC=4,BP=3PC,
∴BP=3,CP=1;设DQ=λ,
则CQ=4-λ;
若△ADQ∽△PCQ,
则
=
,即
=
,
解得:λ=
;
若△ADQ∽△QCP,
则
=
,即
=
,
解得:λ=2,
∴DQ的长为2或
.
 解:如图,∵四边形ABCD为正方形,
解:如图,∵四边形ABCD为正方形,且BC=4,BP=3PC,
∴BP=3,CP=1;设DQ=λ,
则CQ=4-λ;
若△ADQ∽△PCQ,
则
| AD |
| PC |
| DQ |
| CQ |
| 4 |
| 1 |
| λ |
| 4-λ |
解得:λ=
| 16 |
| 5 |
若△ADQ∽△QCP,
则
| AD |
| QC |
| DQ |
| CP |
| 4 |
| 4-λ |
| λ |
| 1 |
解得:λ=2,
∴DQ的长为2或
| 16 |
| 5 |
点评:该题主要考查了正方形的性质、相似三角形的判定及其性质等知识点的应用问题;灵活运用分类讨论的数学思想,数形结合,逐一解析是解题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
武汉冬季某天的最高气温为5℃,最低气温为-3℃,这天的最高气温与最低气温的温差为( )
| A、2℃ | B、-3℃ | C、5℃ | D、8℃ |
由2x-y=6,可以得到用x表示y的式子是( )
| A、y=2x+6 |
| B、y=-2x-6 |
| C、y=2x-6 |
| D、y=-2x+6 |
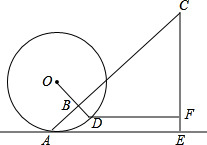 滚铁环是一项老少皆宜的体育运动,如图,铁环⊙O的半径为34cm,且与地面AE切于点A.钩BD的长为4cm,柄BC的长为69cm,且BD⊥BC于点B.某一时刻,DB的延长线经过圆心O,且CB的延长线经过切点A,这时,握手点C离地面的高度CE=
滚铁环是一项老少皆宜的体育运动,如图,铁环⊙O的半径为34cm,且与地面AE切于点A.钩BD的长为4cm,柄BC的长为69cm,且BD⊥BC于点B.某一时刻,DB的延长线经过圆心O,且CB的延长线经过切点A,这时,握手点C离地面的高度CE= 如图是一个8×7的正方形网格图,且每个小正方形的边长为1.
如图是一个8×7的正方形网格图,且每个小正方形的边长为1.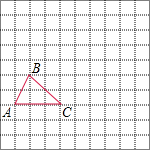 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).