题目内容
计算:
(1)-x2•(-x)2;
(2)(x-2)(x+3);
(3)(a-2b+3c)(a+2b-3c);
(4)(a+
)2•(a2+
)2•(a-
)2.
(1)-x2•(-x)2;
(2)(x-2)(x+3);
(3)(a-2b+3c)(a+2b-3c);
(4)(a+
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
考点:整式的混合运算
专题:计算题
分析:(1)原式利用积的乘方运算法则计算,再利用单项式乘以单项式法则计算即可得到结果;
(2)原式利用多项式乘以多项式法则计算即可得到结果;
(3)原式利用平方差公式化简,再利用完全平方公式展开即可;
(4)原式逆用积的乘方运算法则变形,再利用平方差公式计算即可得到结果.
(2)原式利用多项式乘以多项式法则计算即可得到结果;
(3)原式利用平方差公式化简,再利用完全平方公式展开即可;
(4)原式逆用积的乘方运算法则变形,再利用平方差公式计算即可得到结果.
解答:解:(1)原式=-x4;
(2)原式=x2+3x-2x-6=x2+x-6;
(3)原式=a2-(2b-3c)2=a2-4b2+12bc-9c2;
(4)原式=[(a+
)(a-
)(a2+
)]2=[(a2-
)(a2+
)]2=(a4-
)2=a8-
a4+
.
(2)原式=x2+3x-2x-6=x2+x-6;
(3)原式=a2-(2b-3c)2=a2-4b2+12bc-9c2;
(4)原式=[(a+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 16 |
| 1 |
| 8 |
| 1 |
| 256 |
点评:此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
 如图,线段AB上有C、D两点,以AC、CD、BD为直径的圆的周长分别为C1、C2、C3,以AB为直径的圆的周长为C,下列结论正确的是( )
如图,线段AB上有C、D两点,以AC、CD、BD为直径的圆的周长分别为C1、C2、C3,以AB为直径的圆的周长为C,下列结论正确的是( )| A、C1+C2=C3+C |
| B、C1+C2+C3=C |
| C、C1+C2+C3>C |
| D、C1+C2+C3<C |
关于单项式-x2yz,下列说法正确的是( )
| A、系数是-1,次数是4 |
| B、系数是-1,次数是2 |
| C、系数是0,次数是4 |
| D、系数是0,次数是2 |
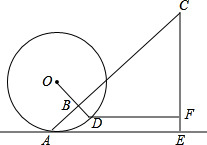 滚铁环是一项老少皆宜的体育运动,如图,铁环⊙O的半径为34cm,且与地面AE切于点A.钩BD的长为4cm,柄BC的长为69cm,且BD⊥BC于点B.某一时刻,DB的延长线经过圆心O,且CB的延长线经过切点A,这时,握手点C离地面的高度CE=
滚铁环是一项老少皆宜的体育运动,如图,铁环⊙O的半径为34cm,且与地面AE切于点A.钩BD的长为4cm,柄BC的长为69cm,且BD⊥BC于点B.某一时刻,DB的延长线经过圆心O,且CB的延长线经过切点A,这时,握手点C离地面的高度CE=