题目内容
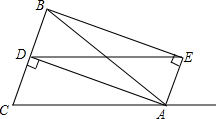 如图,△ABC中,AB=AC,AD⊥BC于点D,AE是∠BAC外角平分线,BE⊥AE,连接DE.
如图,△ABC中,AB=AC,AD⊥BC于点D,AE是∠BAC外角平分线,BE⊥AE,连接DE.(1)求证:DA⊥AE;
(2)求证:四边形DCAE是平行四边形.
考点:平行四边形的判定
专题:证明题
分析:(1)根据三线合一定理证明AD平分∠BAC,然后根据AE是∠BAC外角平分线,即可证得∠DAE=90°,即可证得DA⊥AE;
(2)根据平行四边形的定义即可证得.
(2)根据平行四边形的定义即可证得.
解答: 证明:(1)∵AB=AC,AD⊥BC于点D,
证明:(1)∵AB=AC,AD⊥BC于点D,
∴∠CAD=∠BAD,即∠BAD=
∠BAC,
又∵AE是∠BAC外角平分线,即∠BAE=
∠BAF,
∴∠DAE=∠BAD+∠BAE=
(∠BAC+∠BAF)=90°,
∴DA⊥AE;
(2)∵AD⊥BC,DA⊥AE,
∴BD∥AE,即CD∥AE.
∵BE⊥AE,DA⊥AE,
∴BE∥AD,
∴四边形BDAE是平行四边形.
∴BD=AE,
又∵AB=AC,AD⊥BC,
∴BD=CD,
又∵CD∥AE,
∴四边形DCAE是平行四边形.
 证明:(1)∵AB=AC,AD⊥BC于点D,
证明:(1)∵AB=AC,AD⊥BC于点D,∴∠CAD=∠BAD,即∠BAD=
| 1 |
| 2 |
又∵AE是∠BAC外角平分线,即∠BAE=
| 1 |
| 2 |
∴∠DAE=∠BAD+∠BAE=
| 1 |
| 2 |
∴DA⊥AE;
(2)∵AD⊥BC,DA⊥AE,
∴BD∥AE,即CD∥AE.
∵BE⊥AE,DA⊥AE,
∴BE∥AD,
∴四边形BDAE是平行四边形.
∴BD=AE,
又∵AB=AC,AD⊥BC,
∴BD=CD,
又∵CD∥AE,
∴四边形DCAE是平行四边形.
点评:本题考查了平行四边形的判定与等腰三角形的性质定理,等腰三角形的底边上的中线、高线以及顶角的平分线,三线合一.

练习册系列答案
相关题目
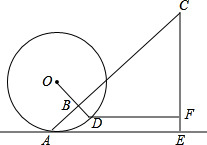 滚铁环是一项老少皆宜的体育运动,如图,铁环⊙O的半径为34cm,且与地面AE切于点A.钩BD的长为4cm,柄BC的长为69cm,且BD⊥BC于点B.某一时刻,DB的延长线经过圆心O,且CB的延长线经过切点A,这时,握手点C离地面的高度CE=
滚铁环是一项老少皆宜的体育运动,如图,铁环⊙O的半径为34cm,且与地面AE切于点A.钩BD的长为4cm,柄BC的长为69cm,且BD⊥BC于点B.某一时刻,DB的延长线经过圆心O,且CB的延长线经过切点A,这时,握手点C离地面的高度CE= 如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,已知点A的坐标为(-4,2),请解答下列问题;
如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,已知点A的坐标为(-4,2),请解答下列问题;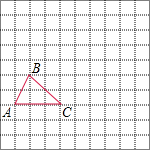 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).