题目内容

12．如图，在?ABCD中，已知AE⊥BC于点E，CF⊥AD于点F．请找出图中与BE相等的线段，并证明你的结论．

分析 由四边形ABCD是平行四边形，AD∥BC，AD=BC，由AE⊥BC于点E，CF⊥AD于点F，可得四边形AECF是平行四边形，即可证得AF=CE，继而证得结论．

解答 解：BE=DF．
理由：∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC，
∵AE⊥BC，CF⊥AD，
∴AE∥CF，
∴四边形AECF是平行四边形，
∴AF=CE，
∵BE=BC-CE，DF=AD-AF，
∴BE=DF．

点评 此题考查了平行四边形的性质以及判定．注意证得AD=BC，AF=CE是关键．

练习册系列答案
相关题目
2．△ABC中，AB＞AC，G为BC的中点，P、A在直线BC的同侧，PG⊥BC，直线BP与直线AC相交于点D，直线CP与直线AB相交于点E，且∠BAC=2∠PBC．
（1）当点P在AB边上时（如图1），E与P重合，D与A重合．则线段BE与线段CD之间的数量关系是BE=CD；
（2）当点P在△ABC内（如图2）时，线段BE与线段CD有何数量关系？证明你的结论；
（3）当∠BAC＞120°（如图3）时，请画出图形，并判断线段BE与线段CD之间的数量关系（直接写出结论，不证明）．
3．下列式子：①-7＜0；②3x+1＞0；③x≥2；④x-6．其中，是不等式的有（　　）
A．①②③B．①②④C．②③④D．①③④
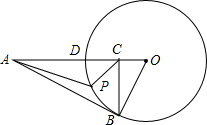20．如图，AB切⊙O于B，BC⊥AO于C，AO交⊙O于D，BO=2，AO=8，P是弧BD上任一点，设k=$\frac{PA}{PC}$，问k的值是否随点P的移动而变化？证明你的结论．
7．如图，在平行四边形ABCD中，DE⊥AB于E，BM=MC=DC，那么∠EMC与∠BEM的大小关系怎样？
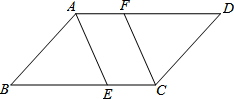17．如图：平行四边形ABCD中，（AB≠AD），AE，CF分别平分∠BAD和∠BCD
①求证：AE=CF；
②若E是BC中点，求证：BC=2AB．
4．使不等式x+7＞4x+9成立的最大整数为-1．
1．如果a＞b，那么下列不等式中一定成立的是（　　）
A．a2＞b2B．1-a＞1-bC．1+a＞1-bD．1+a＞b-1
2．计算：
（1）（$\sqrt{48}$-4$\sqrt{\frac{1}{8}}$）-（3$\sqrt{\frac{1}{3}}$-2$\sqrt{0.5}$）
（2）$（\sqrt{8}+\sqrt{48}）（\sqrt{2}-\sqrt{12}）-{（\sqrt{2}-\sqrt{3}）^2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网