题目内容
7.函数y=$\frac{x-2}{\sqrt{x+1}}$中自变量x的取值范围是( )| A. | x>-1且x≠2 | B. | x≥-1 | C. | x≠-1 | D. | x>-1 |
分析 根据二次根式的性质和分式的意义,被开方数大于等于0,可知x+1≥0;分母不等于0,可知:x+1≠0,则可以求出自变量x的取值范围.
解答 解:根据题意得:$\left\{\begin{array}{l}{x+1≥0}\\{x+1≠0}\end{array}\right.$,
解得:x≥-1且x≠-1,
即x>-1.
故选D.
点评 本题考查的是函数自变量取值范围的求法.函数自变量的范围一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数为非负数.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
19.下列运算正确的是( )
| A. | a8÷a4=a2 | B. | (-3a3)2=6a6 | C. | a3+a5=a8 | D. | a-3•a4=a |
16.太阳中心的温度是19200000℃,用科学记数法可将19200000℃表示为( )
| A. | 1.92×106 | B. | 19.2×106 | C. | 1.92×107 | D. | 0.192×107 |
 如图,点D在△ABC的AB边上.
如图,点D在△ABC的AB边上.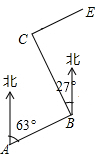 柳林乡要修建一条灌溉水渠,如图,水渠从A村沿北偏东63°方向到B村,从B村沿北偏西27°方向到C村,水渠从C村沿北偏东63°方向修建,可以保持AB的方向一致.
柳林乡要修建一条灌溉水渠,如图,水渠从A村沿北偏东63°方向到B村,从B村沿北偏西27°方向到C村,水渠从C村沿北偏东63°方向修建,可以保持AB的方向一致. 如图,点O是线段AD、BC的中点,连接AB、CD,求证:∠B=∠C.
如图,点O是线段AD、BC的中点,连接AB、CD,求证:∠B=∠C.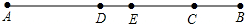 如图所示,线段AB=8cm,E为线段AB的中点,点C为线段EB上一点,且EC=3cm,点D为线段AC的中点,求线段DE的长度.
如图所示,线段AB=8cm,E为线段AB的中点,点C为线段EB上一点,且EC=3cm,点D为线段AC的中点,求线段DE的长度.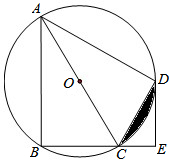 如图,四边形ABCD是⊙O的内接四边形,AC为直径,$\widehat{BD}$=$\widehat{AD}$,DE⊥BC,垂足为E.
如图,四边形ABCD是⊙O的内接四边形,AC为直径,$\widehat{BD}$=$\widehat{AD}$,DE⊥BC,垂足为E.