题目内容
16．一个多边形的所有内角是它的一个外角之和是2000°，那么这个外角是多少度？这个多边形的边数是多少？分析 设多边形的边数为n，多加的外角为α，根据多边形的内角和等于（n-2）•180°，然后解方程即可．
解答 解：设多边形的边数为n，多加的外角为α，
由题意得，（n-2）•180°+α=2000°，
∵11×180°+20°=2000°，
∴n-2=11，α=20°，
∴这个外角是20°，这个多边形的边数是13．
点评 本题考查的是多边形内角和和外角和的知识，掌握多边形的内角和等于（n-2）•180°并根据公式并列出方程是解题的关键．
练习册系列答案
相关题目
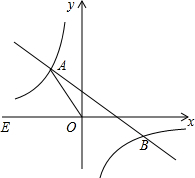在平面直角坐标系xOy中，一次函数y=-$\frac{2}{3}$x+2的图象与反比例函数y=$\frac{k}{x}$（k≠0）的图象交于二、四象限内的A、B两点，若点A纵、横坐标绝对值的比为4：3．
如图，小明不慎将一块三角形模具打碎为两块，他是否可以只带其中的一块碎片到商店去，就能配一块与原来一样的三角形模具呢？如果可以，带哪块去合适？为什么？
7．函数y=$\frac{x-2}{\sqrt{x+1}}$中自变量x的取值范围是（ ）
| A． | x＞-1且x≠2 | B． | x≥-1 | C． | x≠-1 | D． | x＞-1 |