题目内容
4．
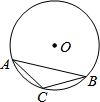如图，△ABC 内接于⊙O，∠A=30°，⊙O的直径为4cm，则点O到BC的距离是（ ）| A． | $\sqrt{3}$cm | B． | $\frac{\sqrt{3}}{2}$cm | C． | $\frac{\sqrt{3}}{3}$cm | D． | 2$\sqrt{3}$cm |
分析 连接OC，OB，并过O点作OD⊥BC于点D，利用圆周角定理易得△BOC为等边三角形，利用锐角三角函数得结果．
解答 
解：连接OC，OB，并过O点作OD⊥BC于点D，
∵∠A=30°，
∴∠BOC=60°，
∵OC=OB，
∴△BOC为等边三角形，
∴∠OCB=60°，
∴OD=OC•sin60°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$（cm），
故选A．
点评 本题主要考查了等边三角形的判定，垂径定理，圆周角定理等，作出适当的辅助线判断出△BOC为等边三角形是解答此题的关键．
练习册系列答案
相关题目
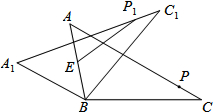如图，在△ABC中，AB=6，BC=8，∠ACB=30°，将△ABC绕点B按逆时针方向旋转，得到△A1BC1．点E为线段AB中点，点P是线段AC上的动点，在△ABC绕点B按逆时针方向旋转的过程中，点P的对应点是点P1，则线段EP1长度的最小值为1．
16．
如图，已知点A，B在半径为1的⊙O上，∠AOB=60°，延长OB至C，过点C作直线OA的垂线记为l，则下列说法正确的是（ ）
如图，已知点A，B在半径为1的⊙O上，∠AOB=60°，延长OB至C，过点C作直线OA的垂线记为l，则下列说法正确的是（ ）| A． | 当BC等于0.5时，l与⊙O相离 | B． | 当BC等于2时，l与⊙O相切 | ||
| C． | 当BC等于1时，l与⊙O相交 | D． | 当BC不为1时，l与⊙O不相切 |
如图，已知△ABC．