题目内容
14.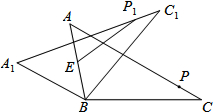 如图,在△ABC中,AB=6,BC=8,∠ACB=30°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转的过程中,点P的对应点是点P1,则线段EP1长度的最小值为1.
如图,在△ABC中,AB=6,BC=8,∠ACB=30°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转的过程中,点P的对应点是点P1,则线段EP1长度的最小值为1.
分析 根据题意可知△ABC绕点B旋转,当AB⊥A1C1时,线段EP1长度的最小,分别根据题意求出P1E和BE的长,进而求出EP1的长.
解答 解:△ABC绕点B旋转,当AB⊥A1C1时,线段EP1长度的最小,
∵∠ACB=30°,
∴∠P1C1B=30°,
在Rt△BP1C1中,
∵BC1=8,
∴BP1=4,
∵E是AB的中点,AB=6,
∴BE=3,
∴P1E=BP1-BE=4-3=1,
故答案为1.
点评 本题主要考查了旋转的性质的知识,解答本题的关键是找出线段EP1长度的最小值的条件:AB⊥A1C1,此题难度一般.

练习册系列答案
相关题目
9.下列平面图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
6.若(a-2)2+(b+3)2=0,则(a+b)2015的值是( )
| A. | 0 | B. | 1 | C. | -l | D. | 2012 |
4.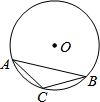 如图,△ABC 内接于⊙O,∠A=30°,⊙O的直径为4cm,则点O到BC的距离是( )
如图,△ABC 内接于⊙O,∠A=30°,⊙O的直径为4cm,则点O到BC的距离是( )
 如图,△ABC 内接于⊙O,∠A=30°,⊙O的直径为4cm,则点O到BC的距离是( )
如图,△ABC 内接于⊙O,∠A=30°,⊙O的直径为4cm,则点O到BC的距离是( )| A. | $\sqrt{3}$cm | B. | $\frac{\sqrt{3}}{2}$cm | C. | $\frac{\sqrt{3}}{3}$cm | D. | 2$\sqrt{3}$cm |
 如图是一些完全相同的小正方体搭成的几何体的三视图.这个几何体只能是( )
如图是一些完全相同的小正方体搭成的几何体的三视图.这个几何体只能是( )



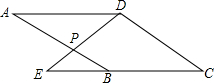 如图,?ABCD中,点P是AB边上的一动点(但不与A,B两点重合),DP的延长线交CB的延长线于点E.
如图,?ABCD中,点P是AB边上的一动点(但不与A,B两点重合),DP的延长线交CB的延长线于点E.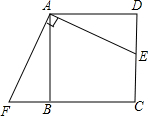 如图,已知E是正方形ABCD中CD上一点,延长BC到点F,使得BF=DE.
如图,已知E是正方形ABCD中CD上一点,延长BC到点F,使得BF=DE.