题目内容
1. 如图,?ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=3,则AB的长是$\sqrt{3}$.
如图,?ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=3,则AB的长是$\sqrt{3}$.
分析 根据直角三角形性质求出CE长,利用勾股定理即可求出AB的长.
解答 解:∵四边形ABCD是平行四边形,
∴AB∥DC,AB=CD,
∵AE∥BD,
∴四边形ABDE是平行四边形,
∴AB=DE=CD,
即D为CE中点,
∵EF⊥BC,
∴∠EFC=90°,
∵AB∥CD,
∴∠DCF=∠ABC=60°,
∴∠CEF=30°,
∵EF=3,
∴CE=$\frac{EF}{cos30°}$=2$\sqrt{3}$,
∴AB=$\sqrt{3}$,
故答案为:$\sqrt{3}$.
点评 本题考查了平行线性质,勾股定理,直角三角形斜边上中线性质,含30度角的直角三角形性质等知识点的应用,此题综合性比较强.

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
 如图,给正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始,第2014次“移位”后,则他所处顶点的编号是3.
如图,给正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始,第2014次“移位”后,则他所处顶点的编号是3. 如图,OP平分∠BOA,∠BOA=45°,PC∥OA,PD⊥OA,若PC=4,则PD等于2$\sqrt{2}$.
如图,OP平分∠BOA,∠BOA=45°,PC∥OA,PD⊥OA,若PC=4,则PD等于2$\sqrt{2}$.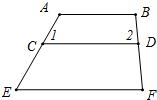 如图,下列六个条件:①∠1=∠E;②∠2=∠F;③∠A+∠1=180°;④∠B+∠2=180°;⑤∠DCE+∠E=180°;⑥∠CDF+∠F=180°,从中选取两个条件作为题设,使得命题“如果∠1=∠E,∠B+∠2=180°,那么AB∥EF”是一个真命题,并证明你的结论.
如图,下列六个条件:①∠1=∠E;②∠2=∠F;③∠A+∠1=180°;④∠B+∠2=180°;⑤∠DCE+∠E=180°;⑥∠CDF+∠F=180°,从中选取两个条件作为题设,使得命题“如果∠1=∠E,∠B+∠2=180°,那么AB∥EF”是一个真命题,并证明你的结论.
 如图,在△ABC中,AD是高,AE是∠BAC的平分线,∠B=70°,∠C=34°,求∠DAE的大小.
如图,在△ABC中,AD是高,AE是∠BAC的平分线,∠B=70°,∠C=34°,求∠DAE的大小.