题目内容
11．
如图，在△ABC中，AD是高，AE是∠BAC的平分线，∠B=70°，∠C=34°，求∠DAE的大小．
分析 根据三角形内角和定理求得∠BAC的度数，则∠EAC即可求解，然后在△ACD中，利用三角形内角和定理求得∠DAC的度数，根据∠DAE=∠DAC-∠EAC即可求解．
解答 解：∵在△ABC中，∠B=70°，∠C=34°，
∴∠BAC=180°-∠B-∠C=180°-70°-34°=76°，
∵AE是∠BAC的平分线，
∴∠EAC=$\frac{1}{2}$∠BAC=38°，
在直角△ADC中，∠DAC=90°-∠C=90°-34°=56°，
∴∠DAE=∠DAC-∠EAC=56°-38°=18°．
点评 本题考查了三角形的内角和定理以及三角形的角平分线的定义，正确理解∠DAE=∠DAC-∠EAC是关键．
练习册系列答案
出彩同步大试卷系列答案
相关题目
如图，?ABCD中，∠ABC=60°，E、F分别在CD和BC的延长线上，AE∥BD，EF⊥BC，EF=3，则AB的长是$\sqrt{3}$．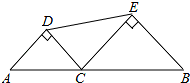
如图，线段AB的长为2，C为AB上一个动点，分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形△ACD和△BCE，那么AC为多长时DE的长最小？最小值为多少？