题目内容
7.解方程组:$\left\{\begin{array}{l}{2x+y=4\\}\\{2y+x=7}\\{2z+x=7}\end{array}\right.$.分析 先由①②解出x与y的值,然后将x的值代入③即可求出z的值.
解答 解:$\left\{\begin{array}{l}{2x+y=4①}\\{2y+x=7②}\\{2z+x=7③}\end{array}\right.$,
①×2-②得:x=$\frac{1}{3}$,
将x=$\frac{1}{3}$代入①得:y=$\frac{10}{3}$,
将x=$\frac{1}{3}$代入③得:z=$\frac{10}{3}$,
∴原方程组的解为:$\left\{\begin{array}{l}{x=\frac{1}{3}}\\{y=\frac{10}{3}}\\{z=\frac{10}{3}}\end{array}\right.$.
点评 此题考查了三元一次方程组的解法,解题的关键是:根据加减消元法由①②解出x与y的值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.如果a是(-8)2的平方根,那么$\root{3}{a}$等于( )
| A. | -8 | B. | -2 | C. | ±8 | D. | ±2 |
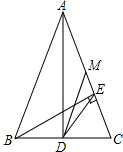 已知:在△ABC中,AB=AC,AD⊥BC,垂足为D,BE⊥AC,垂足为E,M为AC的中点,联结DE、DM,设∠C=α.
已知:在△ABC中,AB=AC,AD⊥BC,垂足为D,BE⊥AC,垂足为E,M为AC的中点,联结DE、DM,设∠C=α.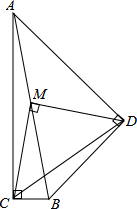 如图,M是Rt△ABC与Rt△ABD的公共边AB的中点,连接CM,DM,恰好△CMD为直角三角形,若BD=6,AD=8,求CD的长.
如图,M是Rt△ABC与Rt△ABD的公共边AB的中点,连接CM,DM,恰好△CMD为直角三角形,若BD=6,AD=8,求CD的长. 如图,?ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=3,则AB的长是$\sqrt{3}$.
如图,?ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=3,则AB的长是$\sqrt{3}$.