题目内容
8.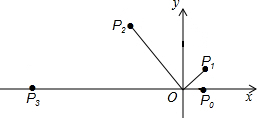 如图,在直角坐标系中,已知点P0的坐标为(1,0),进行如下操作:将线段OP0按逆时针方向旋转60°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转60°,长度伸长为OP1的2倍,得到线段OP2,如此重复操作下去,得到线段OP3,OP4,…则P32的坐标为( )
如图,在直角坐标系中,已知点P0的坐标为(1,0),进行如下操作:将线段OP0按逆时针方向旋转60°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转60°,长度伸长为OP1的2倍,得到线段OP2,如此重复操作下去,得到线段OP3,OP4,…则P32的坐标为( )| A. | (-231,$\sqrt{3}×{2}^{31}$) | B. | (231,$\sqrt{3}×{2}^{31}$) | C. | (-232,$\sqrt{3}×{2}^{32}$) | D. | (232,$\sqrt{3}×{2}^{32}$) |
分析 根据题意得出OP1=2,OP2=4,OP3=8,进而得出P点坐标变化规律,得出点P23的坐标即可.
解答 解:由题意可得出:OP1=2,OP2=4=22,OP3=8=23,
则OP32=232,
∵将线段OP按逆时针方向旋60°,
∴每6个点循环一圈,
∵32÷6=5…2,
∴点P32的坐标与点P2的坐标在第2象限,
∵OP32=232,
∴P32到x轴的距离为:232•sin60°=231•$\sqrt{3}$
到y轴的距离为232•cos60°=231,
∴点P32的坐标是:(-231•,231•$\sqrt{3}$).
故选:A.
点评 此题主要考查了坐标的旋转问题;得到相应的旋转规律及OPn的长度的规律是解决本题的关键.

练习册系列答案
相关题目
18.下面四个QQ表情图案中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
20.关于x的不等式2x-a≤2的解为x≤4.则a的值为( )
| A. | 4 | B. | 6 | C. | -4 | D. | -6 |
18.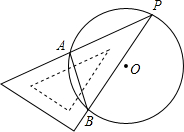 如图,一块直角三角板的30°角的顶点P落在⊙O上,两边分别交⊙O于A、B两点,若⊙O的直径为4,则弦AB长为( )
如图,一块直角三角板的30°角的顶点P落在⊙O上,两边分别交⊙O于A、B两点,若⊙O的直径为4,则弦AB长为( )
 如图,一块直角三角板的30°角的顶点P落在⊙O上,两边分别交⊙O于A、B两点,若⊙O的直径为4,则弦AB长为( )
如图,一块直角三角板的30°角的顶点P落在⊙O上,两边分别交⊙O于A、B两点,若⊙O的直径为4,则弦AB长为( )| A. | 2 | B. | 3 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |