题目内容
13.甲、乙两家体育器材商店出售同样的乒乓球拍和乒乓球,乒乓球拍每副定价60元,乒乓球每盒定价10元,现两家商店都搞促销活动:甲商店规定,每买一副乒乓球拍赠两盒乒球;乙商店规定,所有商品九折优惠,某校乒乓球队需要买两副乒乓球拍,乒乓球若干盒(不少于4盒),设该校要买乒乓球x盒,所需商品在甲商店购买需用y1元,在乙商店购买需用y2元.(1)请分别写出y1、y2与x之间的函数关系式(不必写出x的取值范围)
(2)对x的取值情况进行分析,试说明在哪家商店买所需商品比较合算.
分析 (1)在甲店购买的付款数=2副球拍的总价+(x-4)盒球的总价,在乙店购买的付款数=(2副球拍的总价+x盒球的总价)×0.9,把相关数值代入化简即可;
(2)分别根据y1=y2时,y1>y2时,y1<y2时列出对应式子求解即可.
解答 解:(1)由题意得,
y1=60×2+10(x-4)=10x+80,
y2=(60×2+10x)×0.9=9x+108;
(2)由y1=y2,得10x+80=9x+108,解得x=28,
由y1>y2,得10x+80>9x+108,解得x>28;
由y1<y2,得10x+80<9x+108,解得x<28;
所以,当x=28时,买甲、乙两家商店所需商品收费相同;
当x>28时,选择买乙商店所需商品收费比较合算;
当4≤x<28时,选择买甲商店所需商品收费比较合算.
点评 本题考查了一次函数的应用,解答这类问题时,要先建立函数关系式,然后再分类讨论.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
3.去括号后结果错误的是( )
| A. | (a+2b)=a+2b | B. | -(x-y+z)=-x+y-z | C. | 2(3m-n)=6m-2n | D. | -(a-b)=-a-b |
8.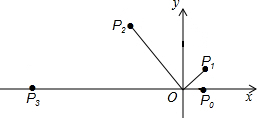 如图,在直角坐标系中,已知点P0的坐标为(1,0),进行如下操作:将线段OP0按逆时针方向旋转60°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转60°,长度伸长为OP1的2倍,得到线段OP2,如此重复操作下去,得到线段OP3,OP4,…则P32的坐标为( )
如图,在直角坐标系中,已知点P0的坐标为(1,0),进行如下操作:将线段OP0按逆时针方向旋转60°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转60°,长度伸长为OP1的2倍,得到线段OP2,如此重复操作下去,得到线段OP3,OP4,…则P32的坐标为( )
 如图,在直角坐标系中,已知点P0的坐标为(1,0),进行如下操作:将线段OP0按逆时针方向旋转60°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转60°,长度伸长为OP1的2倍,得到线段OP2,如此重复操作下去,得到线段OP3,OP4,…则P32的坐标为( )
如图,在直角坐标系中,已知点P0的坐标为(1,0),进行如下操作:将线段OP0按逆时针方向旋转60°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转60°,长度伸长为OP1的2倍,得到线段OP2,如此重复操作下去,得到线段OP3,OP4,…则P32的坐标为( )| A. | (-231,$\sqrt{3}×{2}^{31}$) | B. | (231,$\sqrt{3}×{2}^{31}$) | C. | (-232,$\sqrt{3}×{2}^{32}$) | D. | (232,$\sqrt{3}×{2}^{32}$) |
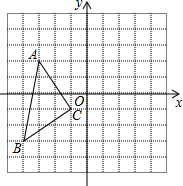 如图,写出△ABC的各顶点坐标,并画出△ABC关于y轴对称的△A1B1C1,并求出△ABC的面积.
如图,写出△ABC的各顶点坐标,并画出△ABC关于y轴对称的△A1B1C1,并求出△ABC的面积.