题目内容
16.在Rt△ABC中,∠C=90°,a=2$\sqrt{6}$,b=6$\sqrt{2}$,求解直角三角形.分析 本题需先求出斜边的长,然后根据ab的长求出∠A的度数,从而求出∠B的度数.
解答 解:在Rt△ABC中,
∵a2+b2=c2,a=2$\sqrt{6}$,b=6$\sqrt{2}$,
∴c=$\sqrt{(2\sqrt{6})^{2}+(6\sqrt{2})^{2}}=4\sqrt{3}$,
∵tan$∠A=\frac{2\sqrt{6}}{6\sqrt{2}}=\frac{\sqrt{3}}{3}$,
∴∠A=30°,
∴∠B=90°-∠A
=90°-30°
=60°.
点评 本题主要考查了解直角三角形的有关知识,在解题时要根据解直角三角形列出式子求出结果是本题的关键.

练习册系列答案
相关题目
6. 如图,在?ABCD中,对角线AC、BD相交于点O,过点O与AD上的一点E作直线OE,交BA的延长线于点F.若AD=4,DC=3,AF=2,则AE的长是( )
如图,在?ABCD中,对角线AC、BD相交于点O,过点O与AD上的一点E作直线OE,交BA的延长线于点F.若AD=4,DC=3,AF=2,则AE的长是( )
 如图,在?ABCD中,对角线AC、BD相交于点O,过点O与AD上的一点E作直线OE,交BA的延长线于点F.若AD=4,DC=3,AF=2,则AE的长是( )
如图,在?ABCD中,对角线AC、BD相交于点O,过点O与AD上的一点E作直线OE,交BA的延长线于点F.若AD=4,DC=3,AF=2,则AE的长是( )| A. | $\frac{7}{8}$ | B. | $\frac{8}{5}$ | C. | $\frac{8}{7}$ | D. | $\frac{3}{2}$ |
7.(1)计算:$\root{3}{{{{(-1)}^2}}}+\root{3}{-8}+\sqrt{3}-|{1-\sqrt{3}}|+\sqrt{2}$
(2)求x的值:25(x+2)2-36=0.
(2)求x的值:25(x+2)2-36=0.
11.将y=x2+4x+1化为y=a(x-h)2+k的形式,h,k的值分别为( )
| A. | 2,-3 | B. | -2,-3 | C. | 2,-5 | D. | -2,-5 |
8.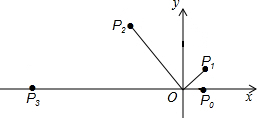 如图,在直角坐标系中,已知点P0的坐标为(1,0),进行如下操作:将线段OP0按逆时针方向旋转60°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转60°,长度伸长为OP1的2倍,得到线段OP2,如此重复操作下去,得到线段OP3,OP4,…则P32的坐标为( )
如图,在直角坐标系中,已知点P0的坐标为(1,0),进行如下操作:将线段OP0按逆时针方向旋转60°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转60°,长度伸长为OP1的2倍,得到线段OP2,如此重复操作下去,得到线段OP3,OP4,…则P32的坐标为( )
 如图,在直角坐标系中,已知点P0的坐标为(1,0),进行如下操作:将线段OP0按逆时针方向旋转60°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转60°,长度伸长为OP1的2倍,得到线段OP2,如此重复操作下去,得到线段OP3,OP4,…则P32的坐标为( )
如图,在直角坐标系中,已知点P0的坐标为(1,0),进行如下操作:将线段OP0按逆时针方向旋转60°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转60°,长度伸长为OP1的2倍,得到线段OP2,如此重复操作下去,得到线段OP3,OP4,…则P32的坐标为( )| A. | (-231,$\sqrt{3}×{2}^{31}$) | B. | (231,$\sqrt{3}×{2}^{31}$) | C. | (-232,$\sqrt{3}×{2}^{32}$) | D. | (232,$\sqrt{3}×{2}^{32}$) |
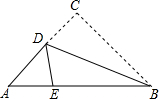 如图的三角形纸片中,AB=8cm,BC=6cm,AC=7cm,沿过点B的直线折叠三角形,使点C落在AB边的点E处,折痕为BD,则△AED的周长为9cm.
如图的三角形纸片中,AB=8cm,BC=6cm,AC=7cm,沿过点B的直线折叠三角形,使点C落在AB边的点E处,折痕为BD,则△AED的周长为9cm.