题目内容
19．将二次函数y=-x2-2x+3化为顶点式y=a（x-h）2+k，则h+k=3．分析 化为一般式后，利用配方法先提出二次项系数，再加上一次项系数的一半的平方来凑完全平方式，把一般式转化为顶点式．
解答 解：y=-x2-2x+3，
y=-（x2+2x+1-1）+3，
y=-（x2+2x+1）+4，
y=-（x+1）2+4，
∴h=-1，k=4，
∴h+k=-1+4=3，
故答案为3．
点评 本题考查了二次函数的三种形式，二次函数的解析式有三种形式：
（1）一般式：y=ax2+bx+c（a≠0，a、b、c为常数）；
（2）顶点式：y=a（x-h）2+k；
（3）交点式（与x轴）：y=a（x-x1）（x-x2）．
练习册系列答案
阅读快车系列答案
相关题目
9．如果向东为正，那么-50m表示的意义是（ ）
| A． | 向东行进50m | B． | 向南行进50m | C． | 向北行进50m | D． | 向西行进50m |
7．（1）计算：$\root{3}{{{{（-1）}^2}}}+\root{3}{-8}+\sqrt{3}-|{1-\sqrt{3}}|+\sqrt{2}$
（2）求x的值：25（x+2）2-36=0．
（2）求x的值：25（x+2）2-36=0．
11．将y=x2+4x+1化为y=a（x-h）2+k的形式，h，k的值分别为（ ）
| A． | 2，-3 | B． | -2，-3 | C． | 2，-5 | D． | -2，-5 |
8．
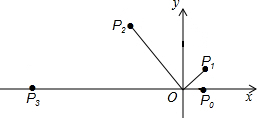如图，在直角坐标系中，已知点P0的坐标为（1，0），进行如下操作：将线段OP0按逆时针方向旋转60°，再将其长度伸长为OP0的2倍，得到线段OP1；又将线段OP1按逆时针方向旋转60°，长度伸长为OP1的2倍，得到线段OP2，如此重复操作下去，得到线段OP3，OP4，…则P32的坐标为（ ）
如图，在直角坐标系中，已知点P0的坐标为（1，0），进行如下操作：将线段OP0按逆时针方向旋转60°，再将其长度伸长为OP0的2倍，得到线段OP1；又将线段OP1按逆时针方向旋转60°，长度伸长为OP1的2倍，得到线段OP2，如此重复操作下去，得到线段OP3，OP4，…则P32的坐标为（ ）| A． | （-231，$\sqrt{3}×{2}^{31}$） | B． | （231，$\sqrt{3}×{2}^{31}$） | C． | （-232，$\sqrt{3}×{2}^{32}$） | D． | （232，$\sqrt{3}×{2}^{32}$） |