题目内容
18．
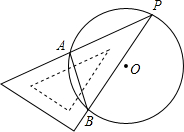如图，一块直角三角板的30°角的顶点P落在⊙O上，两边分别交⊙O于A、B两点，若⊙O的直径为4，则弦AB长为（ ）| A． | 2 | B． | 3 | C． | $\sqrt{2}$ | D． | $\sqrt{3}$ |
分析 连接AO并延长交⊙O于点D，连接BD，根据圆周角定理得出∠D=∠P=30°，∠ABD=90°，再由直角三角形的性质即可得出结论．
解答 
解：连接AO并延长交⊙O于点D，连接BD，
∵∠P=30°，
∴∠D=∠P=30°．
∵AD是⊙O的直径，AD=4，
∴∠ABD=90°，
∴AB=$\frac{1}{2}$AD=2．
故选A．
点评 本题考查的是圆周角定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
8．
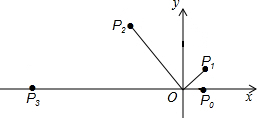如图，在直角坐标系中，已知点P0的坐标为（1，0），进行如下操作：将线段OP0按逆时针方向旋转60°，再将其长度伸长为OP0的2倍，得到线段OP1；又将线段OP1按逆时针方向旋转60°，长度伸长为OP1的2倍，得到线段OP2，如此重复操作下去，得到线段OP3，OP4，…则P32的坐标为（ ）
如图，在直角坐标系中，已知点P0的坐标为（1，0），进行如下操作：将线段OP0按逆时针方向旋转60°，再将其长度伸长为OP0的2倍，得到线段OP1；又将线段OP1按逆时针方向旋转60°，长度伸长为OP1的2倍，得到线段OP2，如此重复操作下去，得到线段OP3，OP4，…则P32的坐标为（ ）| A． | （-231，$\sqrt{3}×{2}^{31}$） | B． | （231，$\sqrt{3}×{2}^{31}$） | C． | （-232，$\sqrt{3}×{2}^{32}$） | D． | （232，$\sqrt{3}×{2}^{32}$） |
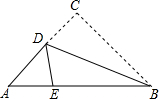如图的三角形纸片中，AB=8cm，BC=6cm，AC=7cm，沿过点B的直线折叠三角形，使点C落在AB边的点E处，折痕为BD，则△AED的周长为9cm．
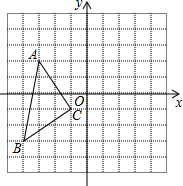如图，写出△ABC的各顶点坐标，并画出△ABC关于y轴对称的△A1B1C1，并求出△ABC的面积．
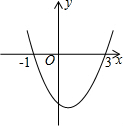已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有如下结论：
如图，在?ABCD中，DF⊥AB于F，DE⊥BC于E，