题目内容
3.某商场销售一批名牌衬衫,平均每天可售出20件,每件赢利50元,为了扩大销售,增加赢利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.求:(1)若商场平均每天要赢利1600元,每件衬衫应降价多少元?
(2)每件衬衫降价多少元时,商场平均每天赢利最多?
分析 (1)若设每件衬衫应降价x元,则每件所得利润为(50-x)元,但每天多售出2x件即售出件数为(20+2x)件,因此每天赢利为(50-x)(20+2x)元,进而可根据题意列出方程求解.
(2)列出商场平均每天赢利y与件衬衫降价x之间的函数关系式,并化为顶点式,即可解答.
解答 解:(1)设每件衬衫应降价x元,
根据题意得(50-x)(20+2x)=1600,
整理得2x2-80x+600=0
解得x1=30,x2=10.
因为要尽量减少库存,在获利相同的条件下,降价越多,销售越快,
故每件衬衫应降30元.
答:每件衬衫应降价30元.
(2)设商场平均每天赢利y元,则
y=(20+2x)(50-x)
=-2x2+80x+1000
=-2(x2-40x-400)=-2[(x-20)2-625]
=-2(x-20)2+1800.
∴当x=120时,y取最大值,最大值为1800.
答:每件衬衫降价20元时,商场平均每天赢利最多,最大利润为1800元.
点评 本题主要考查了二次函数及其应用问题,此类问题是运用数学知识解决现实中的最值问题的常用方法和经典模型,要牢固掌握二次函数的性质;第1小题中降价20元和10元时,每天都赢利1200元,但降价10元不满足“尽量减少库存”,所以做题时应认真审题,不能漏掉任何一个条件.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
7.若实数a,b满足a+b=4,则a2+2ab+b2的值是( )
| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
11.估计$\sqrt{8}$×$\sqrt{\frac{1}{2}}$+$\sqrt{20}$的计算结果应在( )
| A. | 6到7之间 | B. | 7到8之间 | C. | 8到9之间 | D. | 9到10之间 |
 如图,在平面直角坐标系中,A、B均在边长为1的正方形网格格点上
如图,在平面直角坐标系中,A、B均在边长为1的正方形网格格点上 某公司去年年初投资1200万元购买新生产线生产新产品,此外,生产每件该产品还需要成本60元,按规定,该产品售价不得低于100元/件且不超过200元/件,该产品的年销售量y(万件)与产品售价x(元/件)之间的关系如图所示.
某公司去年年初投资1200万元购买新生产线生产新产品,此外,生产每件该产品还需要成本60元,按规定,该产品售价不得低于100元/件且不超过200元/件,该产品的年销售量y(万件)与产品售价x(元/件)之间的关系如图所示.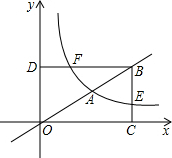 如图,A(2,1)是矩形OCBD的对角线OB上的一点,点E在BC上,双曲线y=$\frac{k}{x}$经过点A,交BC于点E,交BD于点F,若CE=$\frac{2}{3}$.
如图,A(2,1)是矩形OCBD的对角线OB上的一点,点E在BC上,双曲线y=$\frac{k}{x}$经过点A,交BC于点E,交BD于点F,若CE=$\frac{2}{3}$.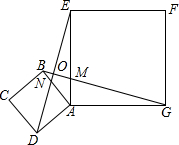 如图,正方形ABCD和正方形AEFG有公共顶点A,连结BG、ED交于点O.猜想BG、ED之间的关系,并证明你的猜想.
如图,正方形ABCD和正方形AEFG有公共顶点A,连结BG、ED交于点O.猜想BG、ED之间的关系,并证明你的猜想. 如图,根据已知条件,直线AB与直线CD平行吗?说说你的理由.
如图,根据已知条件,直线AB与直线CD平行吗?说说你的理由.