题目内容
8.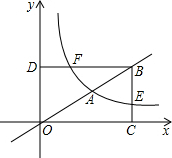 如图,A(2,1)是矩形OCBD的对角线OB上的一点,点E在BC上,双曲线y=$\frac{k}{x}$经过点A,交BC于点E,交BD于点F,若CE=$\frac{2}{3}$.
如图,A(2,1)是矩形OCBD的对角线OB上的一点,点E在BC上,双曲线y=$\frac{k}{x}$经过点A,交BC于点E,交BD于点F,若CE=$\frac{2}{3}$.(1)求双曲线的解析式;
(2)求点F的坐标;
(3)连接EF、DC,求证:EF∥DC.
分析 (1)根据反比例函数图象上点的坐标特征,把A(2,1)代入y=$\frac{k}{x}$中可求出k的值,从而得到双曲线解析式;
(2)先利用待定系数法求出直线解析式为y=$\frac{1}{2}$x,再利用E点的纵坐标为$\frac{2}{3}$和反比例函数图象上点的坐标特征可确定E(3,$\frac{2}{3}$),接着根据一次函数图象上点的坐标特征确定B(3,$\frac{3}{2}$),则F的纵坐标为$\frac{3}{2}$,
然后再利用反比例函数图象上点的坐标特征确定F点坐标;
(3)先得到BD=3,BC=$\frac{3}{2}$,BF=$\frac{5}{3}$,BE=$\frac{5}{6}$,再通过计算得到$\frac{BF}{BD}$=$\frac{BE}{BC}$=$\frac{5}{9}$,加上∠FBE=∠DBC,则可判断△BFE∽△BDC,所以∠BFE=∠BDC,于是可判断EF∥CD.
解答 解:(1)把A(2,1)代入y=$\frac{k}{x}$得k+1×2=2,
所以双曲线解析式为y=$\frac{2}{x}$;
(2)设直线OB解析式为y=ax,
把A(2,1)坐标代入得:1=2a,解得a=$\frac{1}{2}$,
∴直线解析式为y=$\frac{1}{2}$x,
∵四边形OCBD为矩形,CE=$\frac{2}{3}$,
∴E点的纵坐标为$\frac{2}{3}$,
当y=$\frac{2}{3}$时,$\frac{2}{x}$=$\frac{2}{3}$,解得x=3,则E(3,$\frac{2}{3}$),
∴B的横坐标为3,
当x=3时,y=$\frac{1}{2}$x=$\frac{3}{2}$,则B(3,$\frac{3}{2}$),
∴F的纵坐标为$\frac{3}{2}$,
当y=$\frac{3}{2}$时,$\frac{2}{x}$=$\frac{3}{2}$,解得x=$\frac{4}{3}$,
∴F($\frac{4}{3}$,$\frac{3}{2}$);
(3)∵B(3,$\frac{3}{2}$),F($\frac{4}{3}$,$\frac{3}{2}$),E(3,$\frac{2}{3}$),
∴BD=3,BC=$\frac{3}{2}$,BF=3-$\frac{4}{3}$=$\frac{5}{3}$,BE=$\frac{3}{2}$-$\frac{2}{3}$=$\frac{5}{6}$,
∴$\frac{BF}{BD}$=$\frac{5}{9}$,$\frac{BE}{BC}$=$\frac{5}{9}$,
∴$\frac{BF}{BD}$=$\frac{BE}{BC}$,
而∠FBE=∠DBC,
∴△BFE∽△BDC,
∴∠BFE=∠BDC,
∴EF∥CD.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.也考查了矩形的性质和相似三角形的判定与性质.

| A. | $\sqrt{4.84}$ | B. | $\sqrt{0.484}$ | C. | $\sqrt{0.0484}$ | D. | $\sqrt{0.00484}$ |
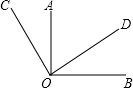 如图,已知OA⊥OB,OC⊥OD,垂足均为点O.求∠BOC+∠AOD的值.
如图,已知OA⊥OB,OC⊥OD,垂足均为点O.求∠BOC+∠AOD的值.