题目内容
7.a是不为1的有理数,我们把$\frac{1}{1-a}$称为a的差倒数.如:2的差倒数是$\frac{1}{1-2}$=-1,-1的差倒数是$\frac{1}{1-(-1)}$=$\frac{1}{2}$.已知a1=$\frac{1}{3}$,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…,依此类推,则a2016=-2.分析 利用规定的运算方法,分别算得a1,a2,a3,a4…找出运算结果的循环规律,利用规律解决问题.
解答 解:∵a1=$\frac{1}{3}$,
a2=$\frac{1}{1-\frac{1}{3}}=\frac{3}{2}$,
a3=$\frac{1}{1-\frac{3}{2}}=-2$,
a4=$\frac{1}{1-(-2)}=\frac{1}{3}$,
…
∴数列以$\frac{1}{3}$,$\frac{3}{2}$,-2三个数依次不断循环,
∵2016÷3=672,
∴a2016=a3=-2.
故答案为:-2
点评 此题考查数字的变化规律,找出数字之间的联系,得出数字之间的运算规律,利用规律解决问题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
17.若△ABC内接于⊙O,∠BOC=130°,则∠A的度数为( )
| A. | 50° | B. | 50°或130° | C. | 65° | D. | 65°或115° |
18. 如图,为估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得
如图,为估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得
BE=20m,EC=10m,CD=20m,则河的宽度AB=( )
 如图,为估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得
如图,为估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=20m,EC=10m,CD=20m,则河的宽度AB=( )
| A. | 60 m | B. | 40 m | C. | 30 m | D. | 20 m |
15.若x<y,则下列不等式中成立的是( )
| A. | 2+x>2+y | B. | 2x>2y | C. | 2-x>2-y | D. | -2x<-2y |
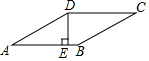 如图,菱形ABCD的高DE是5cm,∠A:∠B=1:5,求∠A的度数及菱形ABCD的面积.
如图,菱形ABCD的高DE是5cm,∠A:∠B=1:5,求∠A的度数及菱形ABCD的面积.