题目内容
18. 如图,为估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得
如图,为估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上.若测得BE=20m,EC=10m,CD=20m,则河的宽度AB=( )
| A. | 60 m | B. | 40 m | C. | 30 m | D. | 20 m |
分析 求出△ABE和△DCE相似,根据相似三角形对应边成比例列式计算即可得解.
解答 解:∵AB⊥BC,CD⊥BC,
∴∠ABE=∠DCE=90°,
又∵∠AEB=∠DEC,
∴△ABE∽△DCE,
∴$\frac{AB}{CD}$=$\frac{BE}{CE}$,
即$\frac{AB}{20}$=$\frac{20}{10}$,
解得AB=40m.
故选B.
点评 本题考查了相似三角形的应用,相似三角形对应边成比例的性质,熟练掌握三角形相似的判定方法是解题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
9.化简x4y4÷(xy)3的结果是( )
| A. | x3y | B. | x2 | C. | xy | D. | x2y |
3.在下列四个标志中,属于轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
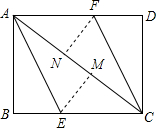 如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处,将边CD沿CF折叠,使点D落在AC上的点N处.
如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处,将边CD沿CF折叠,使点D落在AC上的点N处.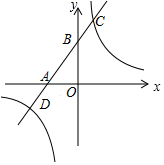 如图,反比例函数y=$\frac{n}{x}$(n为常数,n≠0)的图象与一次函数y=kx+b(k、b为常数,k≠0)的图象在第一象限内交于点C(2,m),一次函数y=kx+b与x轴、y轴分别交于A、B两点.已知tan∠ABO=$\frac{2}{3}$,AB=2$\sqrt{13}$.
如图,反比例函数y=$\frac{n}{x}$(n为常数,n≠0)的图象与一次函数y=kx+b(k、b为常数,k≠0)的图象在第一象限内交于点C(2,m),一次函数y=kx+b与x轴、y轴分别交于A、B两点.已知tan∠ABO=$\frac{2}{3}$,AB=2$\sqrt{13}$.