题目内容
6.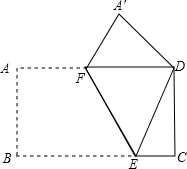 如图,将矩形ABCD沿折痕FE对折,使点B与点D重合,点A落在点A′.
如图,将矩形ABCD沿折痕FE对折,使点B与点D重合,点A落在点A′.(1)求证:△A′FD≌△CED;
(2)求证:A′F=CE.
分析 (1)根据翻折变换的性质和矩形的性质得到∠A′DF=∠EDC,证明△A′FD≌△CDE;
(2)根据全等三角形的性质得到答案.
解答 (1)证明:∵AD∥BC,
∴∠DFE=∠FEB,又∠FEB=∠FED,
∴∠DEF=∠DFE,
∴DF=DE,
∵∠A′DE=∠B=90°,∠FDC=90°,
∴∠A′DF=∠EDC,
在△A′FD和△CDE中,
$\left\{\begin{array}{l}{∠A′=∠DEF}\\{∠A′DF=∠CDE}\\{DF=DE}\end{array}\right.$,
∴△A′FD≌△CDE;
(2)∵△A′FD≌△CDE,
∴A′F=CE.
点评 本题考查的是翻折变换的性质、全等三角形的判定和性质,找准翻折变换中的对应边和对应角是解题的关键,注意全等三角形的判定定理和性质定理的灵活运用.

练习册系列答案
相关题目
16.下列各项正确的个数为( )
①-(-2)2=4;②15=5;③(-1)2n=2n(n为自然数);④(-1)2n+1 =-1(n为自然数):⑤若x2>0,则x>0;⑥若x3<0,则x<0.
①-(-2)2=4;②15=5;③(-1)2n=2n(n为自然数);④(-1)2n+1 =-1(n为自然数):⑤若x2>0,则x>0;⑥若x3<0,则x<0.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
11.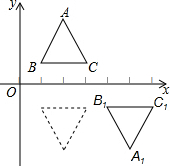 在平面直角坐标系中,把△ABC先沿x轴翻折,再向右平移3个单位得到△A1B1C1现把这两步操作规定为一种变换.如图,已知等边三角形ABC的顶点B、C的坐标分别是(1,1)、(3,1),把三角形经过连续5次这种变换得到三角形△A5B5C5,则点A的对应点A5的坐标是( )
在平面直角坐标系中,把△ABC先沿x轴翻折,再向右平移3个单位得到△A1B1C1现把这两步操作规定为一种变换.如图,已知等边三角形ABC的顶点B、C的坐标分别是(1,1)、(3,1),把三角形经过连续5次这种变换得到三角形△A5B5C5,则点A的对应点A5的坐标是( )
 在平面直角坐标系中,把△ABC先沿x轴翻折,再向右平移3个单位得到△A1B1C1现把这两步操作规定为一种变换.如图,已知等边三角形ABC的顶点B、C的坐标分别是(1,1)、(3,1),把三角形经过连续5次这种变换得到三角形△A5B5C5,则点A的对应点A5的坐标是( )
在平面直角坐标系中,把△ABC先沿x轴翻折,再向右平移3个单位得到△A1B1C1现把这两步操作规定为一种变换.如图,已知等边三角形ABC的顶点B、C的坐标分别是(1,1)、(3,1),把三角形经过连续5次这种变换得到三角形△A5B5C5,则点A的对应点A5的坐标是( )| A. | (5,-$\sqrt{3}$) | B. | (14,1+$\sqrt{3}$) | C. | (17,-1-$\sqrt{3}$) | D. | (20,1+$\sqrt{3}$) |
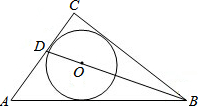 如图,⊙O是Rt△ABC的内切圆,∠C=90°,BO的延长线交BC于D,若BD=10,CD=6,则⊙O半径为$\frac{24}{7}$.
如图,⊙O是Rt△ABC的内切圆,∠C=90°,BO的延长线交BC于D,若BD=10,CD=6,则⊙O半径为$\frac{24}{7}$. 如图,在等边△CDE中,A、B分别是ED、DE延长线上的点,且DE2=AD•EB,求∠ACB的度数.
如图,在等边△CDE中,A、B分别是ED、DE延长线上的点,且DE2=AD•EB,求∠ACB的度数.
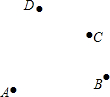 如图,平面上有A、B、C、D4个点,根据下列语句画图.
如图,平面上有A、B、C、D4个点,根据下列语句画图.