题目内容
14.计算二:(1)(-2003)0×2÷$\frac{1}{2}$×[(-$\frac{1}{3}$)2÷23]
(2)(x+2)2-(x-1)(x+1)
(3)(-2x2y+6x3y4-8xy)÷(-2xy)
(4)(x-y+9)(x+y-9)
分析 (1)根据零指数幂的意义以及有理数乘方等运算法则即可求出答案.
(2)根据平方差公式以及完全平方公式即可求出答案.
(3)根据整式除法即可求出答案.
(4)根据平方差公式即可求出答案.
解答 解:(1)原式=1×2×2×($\frac{1}{9}$×$\frac{1}{8}$)
=$\frac{1}{18}$
(2)原式=x2+4x+4-(x2-1)
=4x+5
(3)原式=x-3x2y3+4
(4)原式=[x-(y-9)][x+(y-9)]
=x2-(y-9)2
=x2-(y2-18y+81)
=x2-y2+18y-81
点评 本题考查学生的运算能力,解题的关键是熟练运用运算法则,本题属于基题型.

练习册系列答案
相关题目
2. 如图,AD、BE分别是等边△ABC边BC、AC上的中线,AD、BE相交于点O,则∠AOB的度数为( )
如图,AD、BE分别是等边△ABC边BC、AC上的中线,AD、BE相交于点O,则∠AOB的度数为( )
 如图,AD、BE分别是等边△ABC边BC、AC上的中线,AD、BE相交于点O,则∠AOB的度数为( )
如图,AD、BE分别是等边△ABC边BC、AC上的中线,AD、BE相交于点O,则∠AOB的度数为( )| A. | 120° | B. | 105° | C. | 130° | D. | 135° |
3. 一个大矩形按如图方式分割成九个小矩形,且只有标号为①和②的两个小矩形为正方形,在满足条件的所有分割中.若知道九个小矩形中n个小矩形的周长,就一定能算出这个大矩形的面积,则n的最小值是( )
一个大矩形按如图方式分割成九个小矩形,且只有标号为①和②的两个小矩形为正方形,在满足条件的所有分割中.若知道九个小矩形中n个小矩形的周长,就一定能算出这个大矩形的面积,则n的最小值是( )
 一个大矩形按如图方式分割成九个小矩形,且只有标号为①和②的两个小矩形为正方形,在满足条件的所有分割中.若知道九个小矩形中n个小矩形的周长,就一定能算出这个大矩形的面积,则n的最小值是( )
一个大矩形按如图方式分割成九个小矩形,且只有标号为①和②的两个小矩形为正方形,在满足条件的所有分割中.若知道九个小矩形中n个小矩形的周长,就一定能算出这个大矩形的面积,则n的最小值是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
4.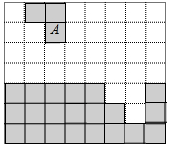 如图,若图形A经过平移与下方图形拼成一个长方形,则正确的平移方式是( )
如图,若图形A经过平移与下方图形拼成一个长方形,则正确的平移方式是( )
 如图,若图形A经过平移与下方图形拼成一个长方形,则正确的平移方式是( )
如图,若图形A经过平移与下方图形拼成一个长方形,则正确的平移方式是( )| A. | 向右平移4格,再向下平移4格 | B. | 向右平移6格,再向下平移5格 | ||
| C. | 向右平移4格,再向下平移3格 | D. | 向右平移5格,再向下平移3格 |

 如图,OP=1,过P作PP1⊥OP且PP1=1,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2…依此法继续作下去,得S△${\;}_{O{P}_{2016}{P}_{2017}}$=$\frac{\sqrt{2017}}{2}$.
如图,OP=1,过P作PP1⊥OP且PP1=1,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2…依此法继续作下去,得S△${\;}_{O{P}_{2016}{P}_{2017}}$=$\frac{\sqrt{2017}}{2}$. 如图,在矩形ABCD中,点E、F分别在边CD、BC上,且DC=3DE=3.将矩形沿直线EF折叠,使点C恰好落在AD边上的点P处,则FP=2$\sqrt{3}$.
如图,在矩形ABCD中,点E、F分别在边CD、BC上,且DC=3DE=3.将矩形沿直线EF折叠,使点C恰好落在AD边上的点P处,则FP=2$\sqrt{3}$.