题目内容
12.(1)计算:$\sqrt{12}-|-\sqrt{3}|$+(π-2015)0-(-1)2015+($\frac{1}{3}$)-2(2)解方程:$\frac{x}{x-2}-1$=$\frac{1}{{x}^{2}-4}$.
分析 (1)原式第一项化为最简二次根式,第二项利用绝对值的代数意义化简,第三项利用零指数幂法则计算,第四项利用乘方的意义计算,最后一项利用负整数指数幂法则计算即可得到结果;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)原式=2$\sqrt{3}$-$\sqrt{3}$+1+1+9=$\sqrt{3}$+11;
(2)去分母得:x2+2x-x2+4=1,
移项合并得:2x=-3,
解得:x=-1.5,
经检验x=-1.5是分式方程的解.
点评 此题考查了实数的运算,以及解分式方程,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
3.已知x、y为实数,且y=$\sqrt{x-8}+\sqrt{8-x}-8$,则x-y的值是( )
| A. | -8 | B. | 0 | C. | 8 | D. | 16 |
20.将一根长1米的木棒,第一次截去一半,第二次截去剩下的一半,如此截下去,截至第五次,剩下的木棒长是( )米.
| A. | $\frac{1}{32}$ | B. | $\frac{1}{16}$ | C. | $\frac{15}{16}$ | D. | $\frac{31}{32}$ |
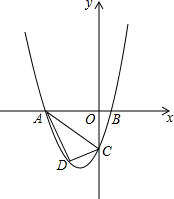 已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=4OB.
已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=4OB.