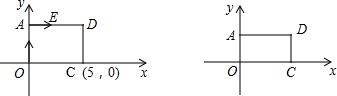题目内容
11.如图(1),在边长为3的等边△ABC上再叠加一个Rt△DEF,在Rt△DEF中,∠DEF=90°,∠F=30°,等边△ABC的边BC与EF重合,顶点E与B重合,定点A在DF上.若等边△ABC沿着EF方向以每秒2个单位的速度运动,直到C与F重合为止.设运动时间x秒,(1)求线段EF的长;
(2)请你用含有x的代数式表示线段AM的长;
(3)假设Rt△DEF和等边△ABC重合部分的面积为y,请你写出y与x之间的函数关系式;
(4)重合部分的面积与Rt△DEF的面积的比有可能是7:24吗?如果有可能,请求出此时x的值;如果没有可能,请说明理由.
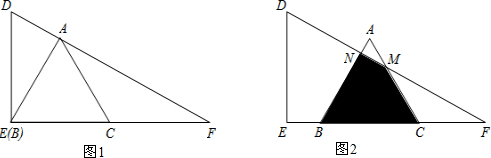
分析 (1)先根据△ABC是等边三角形可知∠ACB=60°,再由三角形外角的性质即可得出∠CAF=30°,故可得出AC=CF=3,故可得出EF的长;
(2)根据速度为2m/s,时间为x秒,可知BE=x,BF=6-x,再由△ABC是等边三角形可知∠A=60°,由∠F=30°得出∠ANM=90°,根据直角三角形的性质得出BN=$\frac{1}{2}$BF=3-x,AN=3-BN=3-(3-x)=$\frac{x}{2}$,再根据M=2AN即可得出结论;
(3)根据(3)中求出的AN、AM的长可用x表示出△AMN的面积,再由y=S△ABC-S△AMN即可得出结论;
(4)根据Rt△DEF中,EF=6,∠F=30°可求出DE的长,进而得出△DEF的面积,再由(3)中y与x的关系式即可得出结论.
解答  解:(1)如图1,∵△ABC是等边三角形,
解:(1)如图1,∵△ABC是等边三角形,
∴∠ACB=60°,
∵∠ACB是△ACF的外角,∠F=30°,
∴∠CAF=∠ACB-∠F=60°-30°=30°,
∴AC=CF=3,
∴EF=BC+CF=3+3=6;
(2)如图2,∵速度为2m/s,时间为x秒,
∴BE=2x,BF=6-2x,
∵△ABC是等边三角形,
∴∠A=60°,
∵∠F=30°,
∴∠ANM=90°,
∴BN=$\frac{1}{2}$BF=$\frac{6-2x}{2}$=3-x;
∴AN=3-BN=3-(3-x)=x,
∵由(1)知,∠AMN=∠F=30°,
∴AM=2AN=2x;
(3)∵由(2)知,AN=x,AM=2x,
∴MN=$\sqrt{3}$x,
∴S△AMN=$\frac{1}{2}$AN•MN=$\frac{1}{2}$×x×$\sqrt{3}$x=$\frac{\sqrt{3}}{2}$x2,
∵△ABC是边长为3的等边三角形,
∴S△ABC=$\frac{1}{2}$×3×$\frac{3\sqrt{3}}{2}$=$\frac{9\sqrt{3}}{4}$,
∴y=S△ABC-S△AMN=$\frac{9\sqrt{3}}{4}$-$\frac{\sqrt{3}}{2}$x2(0≤x≤3);
(4)存在.
∵Rt△DEF中,EF=6,∠F=30°,
∴DE=2$\sqrt{3}$,
∴S△DEF=$\frac{1}{2}$EF•DE=$\frac{1}{2}$×6×2$\sqrt{3}$=6$\sqrt{3}$,
∵由(3)知,y=$\frac{9\sqrt{3}}{4}$-$\frac{\sqrt{3}}{2}$x2(0≤x≤3),
∴$\frac{\frac{9\sqrt{3}}{4}-\frac{\sqrt{3}}{2}{x}^{2}}{6\sqrt{3}}$=$\frac{7}{24}$,
解得:x=1,x=-1(不合题意),
∴当x=1时,存在重合部分的面积与Rt△DEF的面积的比是7:24.
点评 本题考查了相似形综合题,涉及到直角三角形的性质、锐角三角函数的定义、三角形的面积等知识,正确利用锐角三角函数关系得出各边长是解题关键.

 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案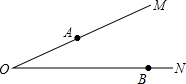 如图,∠MON=20°,A、B分别为射线OM、ON上两定点,且OA=2,OB=4,点P、Q分别为射线OM、ON两动点,当P、Q运动时,线段AQ+PQ+PB的最小值是( )
如图,∠MON=20°,A、B分别为射线OM、ON上两定点,且OA=2,OB=4,点P、Q分别为射线OM、ON两动点,当P、Q运动时,线段AQ+PQ+PB的最小值是( )| A. | 3 | B. | 3$\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
| A. | 绝对值等于本身的数只有1 | B. | a的相反数是-a | ||
| C. | 立方后等于本身的数是-1,0,1 | D. | 任何数与0相乘,都得0 |
| A. | 若a>b,则ac2>bc2 | B. | 若ac2>bc2,则a>b | C. | 若a>b,则a2>b2 | D. | 若a>b,则$\frac{1}{a}$<$\frac{1}{b}$ |
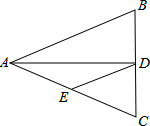 如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为( )
如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,则△CDE的周长为( )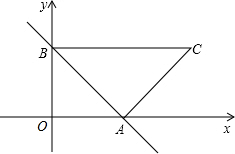 如图,已知在直角坐标系中,A(4,0),B(0,3),以线段AB为直角边在第一象限内作等腰Rt△ABC,∠BAC=90°.点P是x轴上的一个动点,设P(x,0).
如图,已知在直角坐标系中,A(4,0),B(0,3),以线段AB为直角边在第一象限内作等腰Rt△ABC,∠BAC=90°.点P是x轴上的一个动点,设P(x,0).