题目内容
18.如图,在四边形ABCD中,∠ABC+∠ADC=180°,BE、DF分别是∠ABC与∠ADC的平分线,∠ADF与∠AFD互余.(1)证明:BE∥DF;
(2)如图2,延长CB、DF相交于点G,过点B作BH⊥FG,垂足为点H,试判断∠FBH与∠GBH的大小关系,并说明理由.

分析 (1)如图1,先利用角平分线的定义得到∠1=$\frac{1}{2}$∠ABC,∠3=$\frac{1}{2}$∠ADC,则∠1+∠2=90°,加上∠3+∠2=90°,所以∠1=∠2,然后根据平行线的判定方法可得到结论;
(2)先得到∠A=90°,再利用四边形内角和得到∠C=90°,则∠G+∠4=90°,接着证明∠1=∠G,从而可判定△BFG为等腰三角形,然后利用等腰三角形的性质可判断∠FBH=∠GBH.
解答 (1)证明: 如图1,
如图1,
∵BE、DF分别是∠ABC与∠ADC的平分线,
∴∠1=$\frac{1}{2}$∠ABC,∠3=$\frac{1}{2}$∠ADC,
∵∠ABC+∠ADC=180°,
∴∠1+∠2=90°,
∵∠3+∠2=90°,
∴∠1=∠2,
∴BE∥DF;
(2)解:∠FBH=∠GBH.理由如下:
∵∠3+∠2=90°,
∴∠A=90°,
∵∠ABC+∠ADC=180°,
∴∠C=90°,
∴∠G+∠4=90°,
∵∠3=∠4,
∴∠G=∠2,
而∠2=∠1,
∴∠1=∠G,
∴△BFG为等腰三角形,
而BH⊥FG,
∴∠FBH=∠GBH.
点评 本题考查了平行线的判定与性质:性质由形到数,用于推导角的关系并计算;判定由数到形,用于判定两直线平行;性质与判定的已知和结论正好相反,都是角的关系与平行线相关.也考查了等腰三角形的判定与性质.

练习册系列答案
相关题目
9.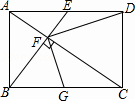 在矩形ABCD中,点E为AD的中点,连接BE,AC,AC⊥BE于点F,连接DF,下列结论.①CF=2AF;②△DEF与△DFA相似;③∠DFC=∠BAC;④当G是BC中点时,有FG=DE,其中正确的个数是( )
在矩形ABCD中,点E为AD的中点,连接BE,AC,AC⊥BE于点F,连接DF,下列结论.①CF=2AF;②△DEF与△DFA相似;③∠DFC=∠BAC;④当G是BC中点时,有FG=DE,其中正确的个数是( )
 在矩形ABCD中,点E为AD的中点,连接BE,AC,AC⊥BE于点F,连接DF,下列结论.①CF=2AF;②△DEF与△DFA相似;③∠DFC=∠BAC;④当G是BC中点时,有FG=DE,其中正确的个数是( )
在矩形ABCD中,点E为AD的中点,连接BE,AC,AC⊥BE于点F,连接DF,下列结论.①CF=2AF;②△DEF与△DFA相似;③∠DFC=∠BAC;④当G是BC中点时,有FG=DE,其中正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
3. 如图,正方形中的数表示该正方形的面积,则字母B所代表的正方形的面积是( )
如图,正方形中的数表示该正方形的面积,则字母B所代表的正方形的面积是( )
 如图,正方形中的数表示该正方形的面积,则字母B所代表的正方形的面积是( )
如图,正方形中的数表示该正方形的面积,则字母B所代表的正方形的面积是( )| A. | 12 | B. | 144 | C. | 13 | D. | 194 |
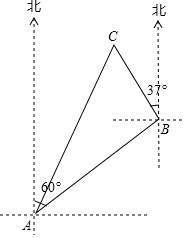 一艘渔船位于港口A的北偏东60°方向,距离港口20海里B处,它沿北偏西37°方向航行至C处突然出现故障,在C处等待救援,B,C之间的距离为10海里,救援船从港口A出发20分钟到达C处,求救援的艇的航行速度.(sin37°≈0.6,cos37°≈0.8,$\sqrt{3}$≈1.732,结果取整数)
一艘渔船位于港口A的北偏东60°方向,距离港口20海里B处,它沿北偏西37°方向航行至C处突然出现故障,在C处等待救援,B,C之间的距离为10海里,救援船从港口A出发20分钟到达C处,求救援的艇的航行速度.(sin37°≈0.6,cos37°≈0.8,$\sqrt{3}$≈1.732,结果取整数)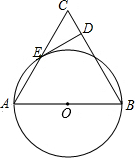 在等边三角形△ABC中,以AB为直径的⊙O与AC交于点E,DE⊥BC于点D.
在等边三角形△ABC中,以AB为直径的⊙O与AC交于点E,DE⊥BC于点D. 如图,正方形ABCD中,点P是BC边上的任意一点(异于端点B,C),连接AP,过点B,D两点作BE⊥AP于点E,DF⊥AP于点F.
如图,正方形ABCD中,点P是BC边上的任意一点(异于端点B,C),连接AP,过点B,D两点作BE⊥AP于点E,DF⊥AP于点F.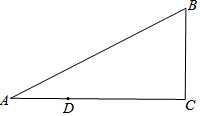 如图,已知△ABC,∠C=90°,点D在线段AC上,且CD=2AD.
如图,已知△ABC,∠C=90°,点D在线段AC上,且CD=2AD.