题目内容
11. 如图,分别以正五边形ABCDE的顶点A,D为圆心,以AB长为半径画$\widehat{BE}$,$\widehat{CE}$.若AB=1,则阴影部分图形的周长为$\frac{6}{5}$π+1(结果保留π).
如图,分别以正五边形ABCDE的顶点A,D为圆心,以AB长为半径画$\widehat{BE}$,$\widehat{CE}$.若AB=1,则阴影部分图形的周长为$\frac{6}{5}$π+1(结果保留π).
分析 由五边形ABCDE可得出,AB=BC=CD=DE=EA=1、∠A=∠D=108°,利用弧长公式可求出$\widehat{BE}$、$\widehat{CE}$的长度,再根据周长的定义,即可求出阴影部分图形的周长.
解答 解:∵五边形ABCDE为正五边形,AB=1,
∴AB=BC=CD=DE=EA=1,∠A=∠D=108°,
∴$\widehat{BE}$=$\widehat{CE}$=$\frac{108°}{180°}$•πAB=$\frac{3}{5}$π,
∴C阴影=$\widehat{BE}$+$\widehat{CE}$+BC=$\frac{6}{5}$π+1.
故答案为:$\frac{6}{5}$π+1.
点评 本题考查了正多边形和圆、弧长公式以及周长的定义,利用弧长公式求出$\widehat{BE}$、$\widehat{CE}$的长度是解题的关键.

练习册系列答案
相关题目
5.下列说法正确的是( )
| A. | 25的平方根是5 | B. | (-3)2的平方根是-3 | ||
| C. | $\frac{9}{25}$的算术平方根是$\frac{3}{5}$ | D. | 0.16的算术平方根是±0.4 |
3. 如图,正方形中的数表示该正方形的面积,则字母B所代表的正方形的面积是( )
如图,正方形中的数表示该正方形的面积,则字母B所代表的正方形的面积是( )
 如图,正方形中的数表示该正方形的面积,则字母B所代表的正方形的面积是( )
如图,正方形中的数表示该正方形的面积,则字母B所代表的正方形的面积是( )| A. | 12 | B. | 144 | C. | 13 | D. | 194 |
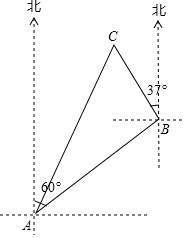 一艘渔船位于港口A的北偏东60°方向,距离港口20海里B处,它沿北偏西37°方向航行至C处突然出现故障,在C处等待救援,B,C之间的距离为10海里,救援船从港口A出发20分钟到达C处,求救援的艇的航行速度.(sin37°≈0.6,cos37°≈0.8,$\sqrt{3}$≈1.732,结果取整数)
一艘渔船位于港口A的北偏东60°方向,距离港口20海里B处,它沿北偏西37°方向航行至C处突然出现故障,在C处等待救援,B,C之间的距离为10海里,救援船从港口A出发20分钟到达C处,求救援的艇的航行速度.(sin37°≈0.6,cos37°≈0.8,$\sqrt{3}$≈1.732,结果取整数)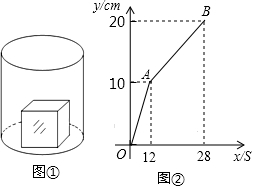 如图①,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,28s时注满水槽.水槽内水面的高度y(cm)与注水时间x(s)之间的函数图象如图②所示.
如图①,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,28s时注满水槽.水槽内水面的高度y(cm)与注水时间x(s)之间的函数图象如图②所示.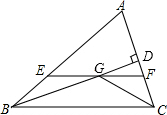 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF∥BC交AB于E,交AC于F,过点G作GD⊥AC于D,下列四个结论:
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF∥BC交AB于E,交AC于F,过点G作GD⊥AC于D,下列四个结论: