题目内容
6.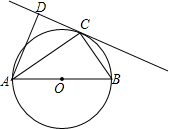 如图,已知△ABC是⊙O的内接三角形,直线CD是⊙O的切线,AC平分∠BAD.
如图,已知△ABC是⊙O的内接三角形,直线CD是⊙O的切线,AC平分∠BAD.(1)求证:AD⊥DC;
(2)若⊙O的半径为5,AC=4$\sqrt{5}$,求AD的长.
分析 (1)连接OC,根据切线性质得到OC∥AD,推出∠DAC=∠OCA=∠CAO,推出OC∥AD,根据平行线的性质即可证得结论;
(2)连接BC,证△DAC∽△CAB,得出比例式,代入求出即可.
解答 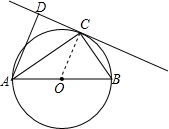 解:(1)连接OC,
解:(1)连接OC,
∵直线CD是⊙O的切线,
∴OC⊥CD,
∵AC平分∠BAD,
∴∠DAC=∠CAB,
∵OA=OC,
∴∠OCA=∠CAB,
∴∠DAC=∠OCA,
∴AD∥OC,
∴AD⊥DC;
(2)∵OC⊥CD,AD⊥DC,
∴∠ADC=∠ACB=90°,
又∵∠DAC=∠CAB,
∴△ADC∽△ACB,
∴$\frac{DA}{AC}$=$\frac{AC}{AB}$,即$\frac{DA}{4\sqrt{5}}$=$\frac{4\sqrt{5}}{10}$,
∴DA=8.
点评 本题考查了切线的性质,相似三角形的性质和判定,平行线性质和判定,等腰三角形性质,主要考查学生的推理能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16. 如图是一个几何体的三视图,则该几何体是( )
如图是一个几何体的三视图,则该几何体是( )
 如图是一个几何体的三视图,则该几何体是( )
如图是一个几何体的三视图,则该几何体是( )| A. | 圆柱 | B. | 圆锥 | C. | 正三棱柱 | D. | 正三棱锥 |
14.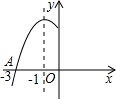 如图,是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为x=-1,给出四个结论:
如图,是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为x=-1,给出四个结论:
①b2>4ac;②2a-b=0;③a+b+c=0;④5a<b.
其中正确结论的个数是( )
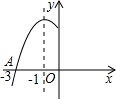 如图,是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为x=-1,给出四个结论:
如图,是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为x=-1,给出四个结论:①b2>4ac;②2a-b=0;③a+b+c=0;④5a<b.
其中正确结论的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18.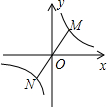 如图,点M(2,a)在反比例函数y=$\frac{6}{x}$的图象上,连结MO并延长交图象的另一分支点N,则线段MN的长是( )
如图,点M(2,a)在反比例函数y=$\frac{6}{x}$的图象上,连结MO并延长交图象的另一分支点N,则线段MN的长是( )
 如图,点M(2,a)在反比例函数y=$\frac{6}{x}$的图象上,连结MO并延长交图象的另一分支点N,则线段MN的长是( )
如图,点M(2,a)在反比例函数y=$\frac{6}{x}$的图象上,连结MO并延长交图象的另一分支点N,则线段MN的长是( )| A. | 3 | B. | $\sqrt{13}$ | C. | 6 | D. | 2$\sqrt{13}$ |
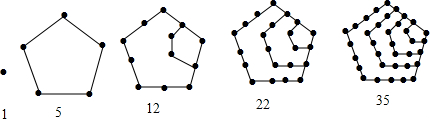
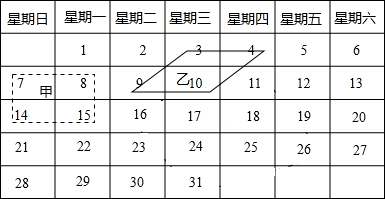
 如图是有关x的代数式的方阵,若第10行第2项的值为1034,则此时x的值为2.
如图是有关x的代数式的方阵,若第10行第2项的值为1034,则此时x的值为2.