题目内容
17.古希腊毕达哥拉斯学派的数学家研究过各种多边形数如“1.5,12.22,35…”这样的数就是五边形数,其规律可用下面的图形表示,则第8个五边形数是92.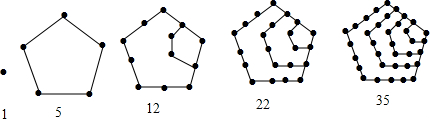
分析 根据前5个五边形数可知,这些正五边形数满足第n个五边形数是$\frac{1}{2}$n(3n-1),据此规律可知第8个正五边形数;.
解答 解:∵第1个数:1=$\frac{1}{2}$×1×(3×1-1);
第2个数:5=$\frac{1}{2}$×2×(3×2-1);
第3个数:12=$\frac{1}{2}$×3×(3×3-1);
第4个数:22=$\frac{1}{2}$×4×(3×4-1);
第5个数:35=$\frac{1}{2}$×5×(3×5-1);
∴第8个数:$\frac{1}{2}$×8×(3×8-1)=92,
故答案为:92.
点评 本题主要考查图形的变化类,将已知图形中点的个数转化成数字的变化规律问题,结合图形从中找出变化规律是关键.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
8.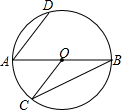 如图,AB是⊙O的直径,点C在圆周上,连结BC、OC,过点A作AD∥OC交⊙O于点D,若∠B=25°,则∠BAD的度数是( )
如图,AB是⊙O的直径,点C在圆周上,连结BC、OC,过点A作AD∥OC交⊙O于点D,若∠B=25°,则∠BAD的度数是( )
 如图,AB是⊙O的直径,点C在圆周上,连结BC、OC,过点A作AD∥OC交⊙O于点D,若∠B=25°,则∠BAD的度数是( )
如图,AB是⊙O的直径,点C在圆周上,连结BC、OC,过点A作AD∥OC交⊙O于点D,若∠B=25°,则∠BAD的度数是( )| A. | 25° | B. | 30° | C. | 40° | D. | 50° |
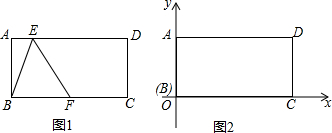
 如图,为了测量教学楼前一棵大树的高度,王明和王亮拿自制的测倾器分别在教学楼AH的二楼C处测得树顶E的仰角为30°,在四楼B处测得大树底部D点的俯角为45°.已知二楼C处离地面高4米,四楼B处离地面高12米.试求树高DE.(参考数据:$\sqrt{3}$≈1.73,结果保留一位小数)
如图,为了测量教学楼前一棵大树的高度,王明和王亮拿自制的测倾器分别在教学楼AH的二楼C处测得树顶E的仰角为30°,在四楼B处测得大树底部D点的俯角为45°.已知二楼C处离地面高4米,四楼B处离地面高12米.试求树高DE.(参考数据:$\sqrt{3}$≈1.73,结果保留一位小数)
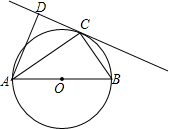 如图,已知△ABC是⊙O的内接三角形,直线CD是⊙O的切线,AC平分∠BAD.
如图,已知△ABC是⊙O的内接三角形,直线CD是⊙O的切线,AC平分∠BAD.