题目内容
18.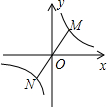 如图,点M(2,a)在反比例函数y=$\frac{6}{x}$的图象上,连结MO并延长交图象的另一分支点N,则线段MN的长是( )
如图,点M(2,a)在反比例函数y=$\frac{6}{x}$的图象上,连结MO并延长交图象的另一分支点N,则线段MN的长是( )| A. | 3 | B. | $\sqrt{13}$ | C. | 6 | D. | 2$\sqrt{13}$ |
分析 先求出M的坐标,根据对称性求出N的坐标,再根据勾股定理求出即可.
解答 解:
过M作x轴的垂线,过N作y轴的垂线,两线交于E,
把(2,a)代入反比例函数y=$\frac{6}{x}$得:a=3,
即M的坐标为(2,3),
所以N的坐标为(-2,-3),
则ME=3-(-3)=6,NE=2-(-2)=4,
所以MN=$\sqrt{{4}^{2}+{6}^{2}}$=2$\sqrt{13}$,
故选D.
点评 本题考查了反比例函数图象上点的坐标特征,勾股定理的应用,能求出M、N的坐标是解此题的关键,数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.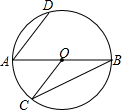 如图,AB是⊙O的直径,点C在圆周上,连结BC、OC,过点A作AD∥OC交⊙O于点D,若∠B=25°,则∠BAD的度数是( )
如图,AB是⊙O的直径,点C在圆周上,连结BC、OC,过点A作AD∥OC交⊙O于点D,若∠B=25°,则∠BAD的度数是( )
 如图,AB是⊙O的直径,点C在圆周上,连结BC、OC,过点A作AD∥OC交⊙O于点D,若∠B=25°,则∠BAD的度数是( )
如图,AB是⊙O的直径,点C在圆周上,连结BC、OC,过点A作AD∥OC交⊙O于点D,若∠B=25°,则∠BAD的度数是( )| A. | 25° | B. | 30° | C. | 40° | D. | 50° |
13.下列运算正确的是( )
| A. | a3+a3=a6 | B. | 4ab÷2a=2ab | C. | a3•a4=a7 | D. | (3x2)3=9x6 |

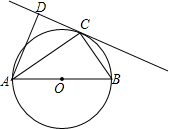 如图,已知△ABC是⊙O的内接三角形,直线CD是⊙O的切线,AC平分∠BAD.
如图,已知△ABC是⊙O的内接三角形,直线CD是⊙O的切线,AC平分∠BAD.