题目内容

12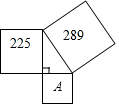．如图，以直角三角形的三边为边向外作正方形，他们的面积依次为225，289，A，则A的值为（　　）
A．4B．8C．16D．64

分析 直接根据勾股定理求解即可．

解答 解：∵以直角三角形的三边为边向外作正方形，他们的面积依次为225，289，A，
∴A=289-225=64．
故选D．

点评 本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．

练习册系列答案
相关题目
2．已知抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于A，B两点，A点位于y轴左侧，B点位于A点右侧，且OA=2，与y轴相交于点C，OC=4，点P为抛物线上的任意一点，且在线段BC的上方．
（1）求抛物线的解析式，并画出图形；
（2）试求当P点运动到什么位置时，△PBC的面积最大并求其最大值；
（3）在抛物线的对称轴上是否存在点Q，使得AQ=CQ？若存在，求出符合条件的Q点坐标；若不存在，请说明理由．
3．完成下面的证明：
如图，已知∠BAG与∠AGD互补，且∠1=∠2，求证：∠E=∠F．
证明：∵∠BAG与∠AGD互补（已知）．
∴AB∥CD（同旁内角互补两直线平行）
∴∠BAG=∠AGC（两直线平行，内错角相等）
又∵∠1=∠2（已知）
∴∠BAG-∠1=∠AGC-∠2（等式的性质）
即∠3=∠4
∴AE∥FG（内错角相等，两直线平行）
∴∠E=∠F（两直线平行，内错角相等）
20．若把分式$\frac{x+y}{3x}$中的x和y都扩大2倍，那么分式的值（　　）
A．扩大2倍B．不变C．缩小2倍D．缩小3倍
7．下列运算正确的是（　　）
A．a3+a4=a7B．2a3•a4=2a7C．（2a）3=6a3D．a8÷a2=a4
17．（1）（$\sqrt{2}$+1）2015（$\sqrt{2}$-1）2014
（2）$\frac{2}{\sqrt{5}+\sqrt{3}}$-$\sqrt{（1-\sqrt{5}）^{2}}$+$\frac{1}{6}$$\sqrt{108}$÷$\frac{1}{2}$$\sqrt{\frac{1}{3}}$．
4．在一个不透明的口袋里装有若干个相同的红球，为了用估计袋中红球的数量，八（1）班学生在数学实验室分组做摸球实验：每组先将10个与红球大小形状完全相同的白球装入袋中，搅匀后从中随机摸出一个球并记下颜色，再把它放回袋中，不断重复．下表是这次活动统计汇总各小组数据后获得的全班数据统计表：
摸球的次数s15030060090012001500
摸到白球的频数n63a247365484606
摸到白球的频率$\frac{n}{s}$0.4200.4100.4120.4060.403b
（1）按表格数据格式，表中的a=123；b=0.404；
（2）请估计：当次数s很大时，摸到白球的频率将会接近0.4（精确到0.1）；
（3）请推算：摸到红球的概率是0.6（精确到0.1）；
（4）试估算：这一个不透明的口袋中红球有15只．
1．给出下列命题：
①在直角三角形ABC中，已知两边长为3和4，则第三边长为5；
②△ABC中，若∠A：∠B：∠C=1：5：6，则△ABC是直角三角形；
③三角形的三边a、b、c满足a2+c2=b2，则△ABC是∠C为直角的直角三角形；
④△ABC中，若 a：b：c=1：2：$\sqrt{3}$，则这个三角形是直角三角形．
其中，正确命题的个数为（　　）
A．1个B．2个C．3个D．4个
2．在平面直角坐标系中，A，B，C三点的坐标分别为（-6，7）、（-3，0）、（0，3）．
（1）画出△ABC，并求△ABC的面积；
（2）在△ABC中，点C经过平移后的对应点为C′（5，4），将△ABC作同样的平移得到△A′B′C′，画出平移后的△A′B′C′，并写出点A′，B′的坐标；
（3）P（-3，m）为△ABC中一点，将点P向右平移4个单位后，再向上平移6个单位得到点Q（n，-3），则m=-9，n=1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网