题目内容
9.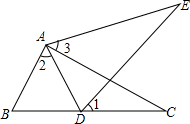 如图,点D在△ABC的边BC上,点E在△ABC的外部,且∠1=∠2=∠3,要使△ABC≌△ADE,还应添加的条件是如:AB=AD等,答案不唯一(写一种即可)
如图,点D在△ABC的边BC上,点E在△ABC的外部,且∠1=∠2=∠3,要使△ABC≌△ADE,还应添加的条件是如:AB=AD等,答案不唯一(写一种即可)
分析 此题是一道开放型的题目,答案不唯一,如AB=AD或AE=AC或BC=DE,求出∠E=∠C,∠BAC=∠DAE,根据全等三角形的判定推出即可.
解答 解:AB=AD,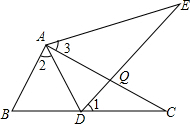
理由是:∵∠3+∠E+∠AQE=180°,∠1+∠C+∠CQD=180°,∠1=∠3,∠AQE=∠CQD,
∴∠E=∠C,
∵∠2=∠3,
∴都加上∠CAD得:∠BAC=∠DAE,
在△ABC和△ADE中
$\left\{\begin{array}{l}{∠C=∠E}\\{∠BAC=∠DAE}\\{AB=AD}\end{array}\right.$
∴△ABC≌△ADE(AAS),
故答案为:AB=AD.
点评 本题考查了三角形内角和定理,全等三角形的判定的应用,能正确运用全等三角形的判定定理进行推理是解此题的关键,全等三角形的判定定理有SAS,AAS,ASA,SSS.

练习册系列答案
相关题目
19.若a,b为有理数,且x=a+b,y=a-b,则x与y的大小关系是( )
| A. | x>y | B. | x=y | C. | x<y | D. | 不能确定 |
4.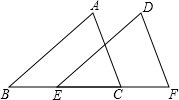 如图,已知AB=DE,BE=CF,添加下列中一个条件还不能使△ABC≌△DEF的是( )
如图,已知AB=DE,BE=CF,添加下列中一个条件还不能使△ABC≌△DEF的是( )
 如图,已知AB=DE,BE=CF,添加下列中一个条件还不能使△ABC≌△DEF的是( )
如图,已知AB=DE,BE=CF,添加下列中一个条件还不能使△ABC≌△DEF的是( )| A. | AC=DF | B. | ∠B=∠DEF | C. | ∠A=∠D=90° | D. | ∠ACB=∠F |
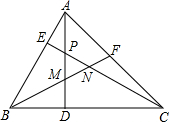 如图所示,△ABC中,∠ABC=60°,∠BAC=75°,AD⊥BC,CE⊥AB,垂足分别为D、E,AD与CE相交于点P,∠ABC的平分线BF分别交AD、CE、AC于点M、N、F.
如图所示,△ABC中,∠ABC=60°,∠BAC=75°,AD⊥BC,CE⊥AB,垂足分别为D、E,AD与CE相交于点P,∠ABC的平分线BF分别交AD、CE、AC于点M、N、F.