题目内容
20.计算:(1)3$\sqrt{18}$+$\frac{1}{5}$$\sqrt{50}$-4$\sqrt{\frac{1}{2}}$
(2)($\sqrt{6}$-$\sqrt{18}$)2+3$\sqrt{48}$.
分析 (1)首先化简二次根式进而合并同类二次根式得出答案;
(2)首先化简二次根式进而合并同类二次根式得出答案.
解答 解:(1)原式=9$\sqrt{2}$+$\sqrt{2}$-2$\sqrt{2}$=8$\sqrt{2}$;
(2)原式=($\sqrt{6}$)2-2×$\sqrt{6}$×3$\sqrt{2}$+($\sqrt{18}$)2+12$\sqrt{3}$
=6-12$\sqrt{3}$+18+12$\sqrt{3}$
=24.
点评 此题主要考查了二次根式的混合运算,正确化简二次根式是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.下列代数式中单项式共有( )
$\frac{{x}^{2}-3}{5}$,-xy2,-0.5,$\frac{a}{3}$,$\frac{1}{x-y}$,ax2+bx+c,a2b3,$\frac{ab}{5}$.
$\frac{{x}^{2}-3}{5}$,-xy2,-0.5,$\frac{a}{3}$,$\frac{1}{x-y}$,ax2+bx+c,a2b3,$\frac{ab}{5}$.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
8.根据学校合唱比赛的活动细则,每个参赛的合唱团在比赛时须演唱4首歌曲,九(2)班合唱团已确定了2首歌曲,还需在A,B两首歌曲中确定一首,在C、D、E三首歌曲中确定另一首,则确定的参赛歌曲中有一首是D的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
15. 课间操时,小华、小军、小刚的位置如图,如果小华的位置用(0,0)表示,小军的位置用(2,1)表示,那么小刚的位置可以表示成( )
课间操时,小华、小军、小刚的位置如图,如果小华的位置用(0,0)表示,小军的位置用(2,1)表示,那么小刚的位置可以表示成( )
 课间操时,小华、小军、小刚的位置如图,如果小华的位置用(0,0)表示,小军的位置用(2,1)表示,那么小刚的位置可以表示成( )
课间操时,小华、小军、小刚的位置如图,如果小华的位置用(0,0)表示,小军的位置用(2,1)表示,那么小刚的位置可以表示成( )| A. | (4,3) | B. | (4,5) | C. | (3,4) | D. | (5,4) |
10.如果一个有理数的奇次幂是正数,那么这个有理数( )
| A. | 一定是正数 | B. | 是正数或负数 | ||
| C. | 一定是负数 | D. | 可以是任意有理数 |
 如图,△ABC是⊙O的内接三角形,CE是⊙O的直径,CF是⊙O的弦,CF⊥AB,垂足为D,若∠BCE=20°,求∠ACF的度数.
如图,△ABC是⊙O的内接三角形,CE是⊙O的直径,CF是⊙O的弦,CF⊥AB,垂足为D,若∠BCE=20°,求∠ACF的度数.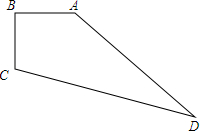 如图,在四边形地块ABCD中,∠B=90°,AB=30m,BC=40m,CD=130m,AD=120m,求这块地的面积.
如图,在四边形地块ABCD中,∠B=90°,AB=30m,BC=40m,CD=130m,AD=120m,求这块地的面积.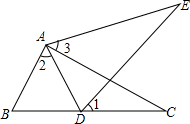 如图,点D在△ABC的边BC上,点E在△ABC的外部,且∠1=∠2=∠3,要使△ABC≌△ADE,还应添加的条件是如:AB=AD等,答案不唯一(写一种即可)
如图,点D在△ABC的边BC上,点E在△ABC的外部,且∠1=∠2=∠3,要使△ABC≌△ADE,还应添加的条件是如:AB=AD等,答案不唯一(写一种即可)